观察下图:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…
则第________行的各数之和等于20112.
1006
分析:由已知,得出第n行的第一个数是n,该行共有2n-1个数字,且构成以1为公差的等差数列,根据等差数列前n项和公式,得出关于n的方程求出行数n即可.
解答:此图各行的数字排布规律是:第n行的第一个数是n,该行共有2n-1个数字,且构成以1为公差的等差数列.
所以第n行的各数之和为(2n-1)•n+
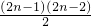
=4n
2-4n+1,
由4n
2-4n+1=2011
2,得 4n(n-1)=2011
2-1
2=2012×2010=(2×1006)×(2×1005)=4×1006×1005
n=1006,
故答案为:1006.
点评:本题考查等差数列前n项和公式的应用,得出图中各行数的排布规律是关键.考查抽象概括、计算能力.本题解关于n的方程时,对因式进行分解、对应.

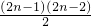 =4n2-4n+1,
=4n2-4n+1,
