
分析 根据函数的定义域和值域的求法进行i区就即可.
解答 解:(1)y=2x+1的定义域为(-∞,+∞),
∵2x>0,∴y=2x+1>1,即函数的值域为(1,+∞);
(2)由5x-1≥0得x≥$\frac{1}{5}$,即函数的定义域为[$\frac{1}{5}$,+∞),
∵$\sqrt{5x-1}$≥0,
∴y=3${\;}^{\sqrt{5x-1}}$≥30=1,即函数的值域为[1,+∞);
(3)由x-1≠0得x≠1,即函数的定义域为(-∞,1)∪(1,+∞),
∵$\frac{1}{x-1}$≠0,
∴y=0.4${\;}^{\frac{1}{x-1}}$>0且y≠1.
即函数的值域为(0,1)∪(1,+∞).
点评 本题主要考查函数的定义域和值域的求解,要求熟练掌握常见函数成立的条件.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
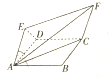 某几何体如图所示,底面ABCD是边长为2的正方形,ACFE是平行四边形,AE=2,∠EAB=∠EAD=60°.
某几何体如图所示,底面ABCD是边长为2的正方形,ACFE是平行四边形,AE=2,∠EAB=∠EAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 纵坐标不变,横坐标伸长为原来的3倍,再将所得图象向右平移$\frac{π}{9}$个单位 | |
| B. | 纵坐标不变,横坐标伸长为原来的3倍,再将所得图象向右平移$\frac{π}{3}$个单位 | |
| C. | 纵坐标不变,横坐标缩短为原来的$\frac{1}{3}$,再将所得图象向右平移$\frac{π}{3}$个单位 | |
| D. | 纵坐标不变,横坐标缩短为原来的$\frac{1}{3}$,再将所得图象向右平移$\frac{π}{9}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com