
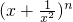 (n∈N+)的展开式中存在常数项A,此时二项式系数的最大值为B,则
(n∈N+)的展开式中存在常数项A,此时二项式系数的最大值为B,则 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,BQ=BR,点S、D、A、Q共线及P、D、C、R共线.
如图某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,BQ=BR,点S、D、A、Q共线及P、D、C、R共线.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
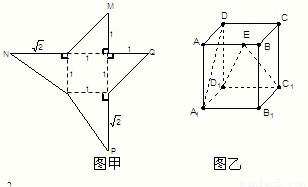
 (2010•龙岩二模)图甲是一个几何体的表面展开图,图乙是棱长为1cm的正方体.
(2010•龙岩二模)图甲是一个几何体的表面展开图,图乙是棱长为1cm的正方体.查看答案和解析>>
科目:高中数学 来源:2010年福建省龙岩市高考数学二模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com