名校联盟快乐课堂系列答案
黄冈创优卷系列答案科目：高中数学 来源： 题型：
（本小题满分12分）
个正数排成一个
行列的数阵：
| 第1列 | 第2列 | 第3列 | … | 第 | |
| 第1行 |
|
|
| … |
|
| 第2行 |
|
|
| … |
|
| 第3行 |
|
|
| … |
|
| … | … | … | … | … | … |
| 第 |
|
|
| … |
|
其中
表示该数阵中位于第
行第
列的数。已知该数阵每一行的数成等差数列，每一列的数成公比为2的等比数列，
（1）求
； （2）设
，求
；
（3）在（2）的条件下，若不等式
对任意的
恒成立，求
的最大值。
查看答案和解析>>
科目：高中数学 来源： 题型：
（湖南卷理21）已知函数f(x)=ln2(1+x)-
.
(I ) 求函数
的单调区间;
（Ⅱ）若不等式
对任意的
都成立（其中e是自然对数的底数）.求
的最大值.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年辽宁省五校协作体高三上学期期中考试理科数学试卷（解析版） 题型：解答题
已知函数
．
（1）证明函数
在区间
上单调递减；
（2）若不等式
对任意的
都成立，（其中
是自然对数的底数），求实数
的最大值．
查看答案和解析>>
科目：高中数学 来源：2012-2013学年福建省高三上学期期中理科数学试卷（解析版） 题型：解答题
（本小题满分15分）
已知函数
（Ⅰ）求函数
的单调区间；
（Ⅱ）若
，试分别解答以下两小题.
（ⅰ）若不等式
对任意的
恒成立，求实数
的取值范围；
（ⅱ）若
是两个不相等的正数，且
，求证：
．
查看答案和解析>>
科目：高中数学 来源：2011-2012学年河南省豫东、豫北十所名校高三测试理科数学试卷（解析版） 题型：解答题
对定义在区间l，上的函数
，若存在开区间
和常数C，使得对任意的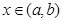
都有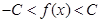
，且对任意的x
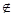（a，b）都有
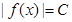恒成立，则称函数为区间I上的“Z型”函数．
（I）求证：函数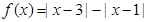
是R上的“Z型”函数；
（Ⅱ）设是（I）中的“Z型”函数，若不等式
对任意的x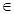
R恒成立，求实数t的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
对任意的
、
恒成立，则正实数
的最小值为
，故选择C。
