
已知函数 ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程 +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数 的取值范围;
的取值范围;
(3)若关于x的方程 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解 ,求k的取值范围。
,求k的取值范围。
(1) (2)
(2) (3)
(3)
【解析】本试题主要是考查了函数与方程的思想的综合运用。
(1) ,
, +3即
+3即 ,对于定义域分段讨论得到解的情况。
,对于定义域分段讨论得到解的情况。
(2)因为 是定义域(0,2)上的单调函数,结合函数与图像的关系式得到结论。
是定义域(0,2)上的单调函数,结合函数与图像的关系式得到结论。
(3)关于x的方程 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解 ,那么借助于图像得到结论。
,那么借助于图像得到结论。
解(1) ,
, +3即
+3即
当 时,
时, ,此时该方程无解. ……1分
,此时该方程无解. ……1分
当 时,
时, ,原方程等价于:
,原方程等价于: 此时该方程的解为
此时该方程的解为 .
.
综上可知:方程 +3在(0,2)上的解为
+3在(0,2)上的解为 .……3分
.……3分
(2)
 ,
,
 ………4分
………4分
 ,…………5分
,…………5分
可得:若 是单调递增函数,则
是单调递增函数,则
 …6分
…6分
若 是单调递减函数,则
是单调递减函数,则
 ,………7分
,………7分
综上可知: 是单调函数时
是单调函数时 的取值范围为
的取值范围为 .…8分
.…8分
(2)[解法一]:当 时,
时, ,①
,①
当 时,
时, ,②
,②
若k=0则①无解,②的解为 故
故 不合题意。…………9分
不合题意。…………9分
若 则①的解为
则①的解为 ,
,
(Ⅰ)当 时,
时, 时,方程②中
时,方程②中
故方程②中一根在(1,2)内另一根不在(1,2)内,…………10分
设 ,而
,而 则
则 又
又 ,故
,故 ,………11分
,………11分
(Ⅱ)当 时,即
时,即 或
或 0时,方程②在(1,2)须有两个不同解,12分
0时,方程②在(1,2)须有两个不同解,12分
而 ,知方程②必有负根,不合题意。……13分
,知方程②必有负根,不合题意。……13分
综上所述, ………14分
………14分
[略解法二] ,………9分
,………9分
 ,
, ………10分
………10分
分析函数的单调性及其取值情况易得解(用图象法做,必须画出草图,再用必要文字说明)……………13分
利用该分段函数的图象得 ……………………14分
……………………14分


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:2011届辽宁省沈阳二中高三第二次阶段测试理科数学卷 题型:填空题
已知函数 与
与 的定义域为
的定义域为 ,有下列5个命题:
,有下列5个命题:
①若 ,则
,则 的图象自身关于直线
的图象自身关于直线 轴对称;
轴对称;
② 与
与 的图象关于直线
的图象关于直线 对称;
对称;
③函数 与
与 的图象关于
的图象关于 轴对称;
轴对称;
④ 为奇函数,且
为奇函数,且 图象关于直线
图象关于直线 对称,则
对称,则 周期为2;
周期为2;
⑤ 为偶函数,
为偶函数, 为奇函数,且
为奇函数,且 ,则
,则 周期为2。
周期为2。
其中正确命题的序号为 。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省高三第二次阶段测试文科数学卷 题型:填空题
已知函数 与
与 的定义域为
的定义域为 ,有下列5个命题:
,有下列5个命题:
①若 ,则
,则 的图象自身关于直线
的图象自身关于直线 轴对称;
轴对称;
② 与
与 的图象关于直线
的图象关于直线 对称;
对称;
③函数 与
与 的图象关于
的图象关于 轴对称;
轴对称;
④ 为奇函数,且
为奇函数,且 图象关于直线
图象关于直线 对称,则
对称,则 周期为2;
周期为2;
⑤ 为偶函数,
为偶函数, 为奇函数,且
为奇函数,且 ,则
,则 周期为2。
周期为2。
其中正确命题的序号为 。
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二上学期期中理科数学试卷 题型:解答题
已知函数 ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程 +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数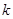 的取值范围;
的取值范围;
(3)若关于x的方程 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解 ,求k的取值范围。
,求k的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知函数![]() ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程![]() +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若![]() 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于x的方程![]() 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解![]() ,求k的取值范围。
,求k的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com