
设甲、乙、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标的概率.
0.94 0.44
【解析】
解:设Ak表示“第k人命中目标”,k=1,2,3.
这里,A1,A2,A3独立,且P(A1)=0.7,P(A2)=0.6,P(A3)=0.5.
从而,至少有一人命中目标的概率为1-P(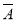 1·
1·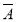 2·
2·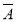 3)=1-P(
3)=1-P(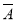 1)P(
1)P(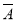 2)P(
2)P( 3)=1-0.3×0.4×0.5=0.94.
3)=1-0.3×0.4×0.5=0.94.
恰有两人命中目标的概率为
P(A1·A2·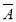 3+A1·
3+A1·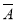 2·A3+
2·A3+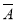 1·A2·A3)
1·A2·A3)
=P(A1·A2· 3)+P(A1·
3)+P(A1·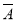 2·A3)+P(
2·A3)+P(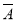 1·A2·A3)
1·A2·A3)
=P(A1)P(A2)P(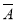 3)+P(A1)P(
3)+P(A1)P( 2)P(A3)+
2)P(A3)+
P( 1)P(A2)P(A3)=0.7×0.6×0.5+0.7×0.4×0.5+0.3×0.6×0.5=0.44.
1)P(A2)P(A3)=0.7×0.6×0.5+0.7×0.4×0.5+0.3×0.6×0.5=0.44.
∴至少有一人命中目标的概率为0.94,恰有两人命中目标的概率为0.44.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2章练习卷(解析版) 题型:解答题
某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是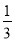 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:填空题
设随机变量X的分布列为P(X=k)=pk(1-p)1-k(k=0.1,0<p<1),则E(X)=________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.4练习卷(解析版) 题型:填空题
已知一个射手每次击中目标的概率为p=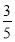 ,他在4次射击中,命中两次的概率为________,刚好在第二、第三两次击中目标的概率为________.
,他在4次射击中,命中两次的概率为________,刚好在第二、第三两次击中目标的概率为________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.3练习卷(解析版) 题型:解答题
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”,则该课程考核“合格”,若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7,在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.3练习卷(解析版) 题型:解答题
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.3练习卷(解析版) 题型:解答题
某种动物由出生算起活到20岁的概率为0.8,活到25岁的概率为0.4,现有一个20岁的动物,求它能活到25岁的概率.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.2练习卷(解析版) 题型:填空题
某学校从4名男生和2名女生中任选3人作为参加上海世博会的志愿者,设随机变量X表示所选3人中女生的人数,则P(X≥1)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com