
分析 (1)求出f′(x)且f′(x)=0有两个不同的正根,即x2-ax+a=0两个不同的正根,即可求实数a的取值范围;
(2)利用韦达定理,可得$\frac{f({x}_{1})+f({x}_{2})}{{x}_{1}+{x}_{2}}$=lna-$\frac{1}{2}$a-1,构造函数,确定函数的单调性,求出其范围,即可求Ψ的最小值.
解答 解:(1)由题设知,函数f(x)的定义域为(0,+∞),
f′(x)=$\frac{{x}^{2}-ax+a}{x}$且f′(x)=0有两个不同的正根,
即x2-ax+a=0两个不同的正根x1,x2,(x1<x2)
则 $\left\{\begin{array}{l}{△{=a}^{2}-4a>0}\\{a>0}\end{array}\right.$,∴a>4,
(0,x1),f′(x)>0,(x1,x2),f′(x)<0,(x2,+∞),f′(x)>0,
∴x1,x2是f(x)的两个极值点,符合题意,
∴a>4;
(2)f(x1)+f(x2)=alnx1+$\frac{1}{2}$x12-ax1+alnx2+$\frac{1}{2}$x22-ax2=a(lna-$\frac{1}{2}$a-1),
∴$\frac{f({x}_{1})+f({x}_{2})}{{x}_{1}+{x}_{2}}$=lna-$\frac{1}{2}$a-1,
令y=lna-$\frac{1}{2}$a-1,则y′=$\frac{1}{a}$-$\frac{1}{2}$,
∵a>4,
∴y′<0,
∴y=lna-$\frac{1}{2}$a-1在(4,+∞)上单调递减,
∴y<ln4-3,
∴Ψ的取值范围是[ln4-3,+∞).
点评 本题考查导数知识的综合运用,考查函数的极值,考查不等式恒成立问题,考查学生分析解决问题的能力,属于中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
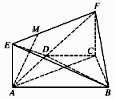 如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.
如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com