解:(1)根据题意,当销售利润为4万元,销售量为4÷(5-4)=4(万瓶).
答:销售量x为4万瓶时销售利润为4万元.
(2)点A的坐标为(4,4),从13日到15日利润为5.5-4=1.5(万元),
所以销售量为1.5÷(5.5-4)=1(万瓶),所以点B的坐标为(5,5.5).
设线段AB所对应的函数关系式为y=kx+b,则

,解得
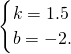
,
∴线段AB所对应的函数关系式为y=1.5x-2(4≤x≤5).
从15日到31日销售5万瓶,利润为1×1.5+4×(5.5-4.5)=5.5(万元).
∴本月销售该饮料的利润为5.5+5.5=11(万元),所以点C的坐标为(10,11).
设线段BC所对应的函数关系式为y=mx+n,则

,解得
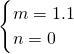
,
所以线段所对应的函数关系式为y=1.1x(5≤x≤10).
(3)线段AB倾斜度最大,所以利润率最高.
分析:(1)根据销售记录每升利润为1元,所以销售利润为4万元时销售量为4万升;
(2)设BC所对应的函数关系式为y=kx+b,求出图象中B点和C点的坐标代入关系式中即可.
(3)判断利润率最大,应该看倾斜度.
点评:这是一道分段函数难度中上的考题,主要考查从图表获取信息和利用一次函数解决实际问题的能力.本题的关键是要仔细审题,找出数量变化与对应函数图象的关系,思考:线段AB,OA,
BC对应的函数有哪些不同其根本原因是每升的成本,利润的变化,导致销售量的变化,正确计算出三种情形中的每升利润,是解决这一分段函数的重中之重.


 ,解得
,解得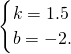 ,
, ,解得
,解得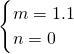 ,
,


