
已知函数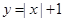 ,
,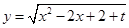 ,
,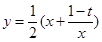
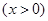 的最小值恰好是方程
的最小值恰好是方程 的三个根,其中
的三个根,其中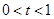 。
。
(1)求证: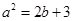 ;
;
(2)设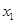 ,
,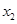 是函数
是函数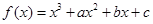 的两个极值点。若
的两个极值点。若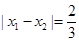 ,求函数
,求函数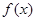 的解析式。
的解析式。
(1)见解析(2)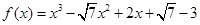
【解析】解:(1)三个函数的最小值依次为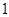 ,
,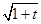 ,
,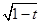 ,由
,由 ,得
,得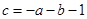
∴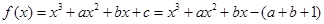
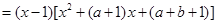 ,
,
故方程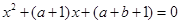 的两根是
的两根是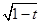 ,
,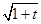 。
。
故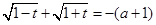 ,
,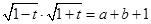 。
。
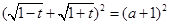 ,即
,即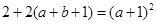 ∴
∴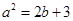 。
。
(2)①依题意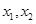 是方程
是方程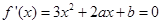 的根,故有
的根,故有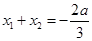 ,
,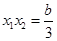 ,
,
且△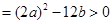 ,得
,得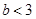 。
。
由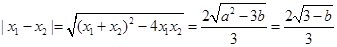
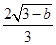
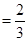 ;得,
;得,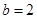 ,
,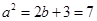 。
。
由(1)知 ,故
,故 ,
,
∴  ,
,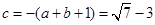 ∴
∴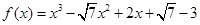
本试题主要是考查了函数的最值的运用,以及导数在研究函数中的极值的运用,和函数解析式的求解的综合问题。
(1)根据已知条件得到三个最小值,然后代入到三次方程中的,到系数a,b,c的关系式。
(2)依题意可知求解原函数的导函数,说明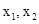 是导函数为零的方程的两个根,然后利用韦达定理得到参数a,b的关系式,进而得到a的范围,从而确定a的值和b的值,求解得到解析式。
是导函数为零的方程的两个根,然后利用韦达定理得到参数a,b的关系式,进而得到a的范围,从而确定a的值和b的值,求解得到解析式。


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com