等腰三角形一腰所在直线l1的方程是x-2y-2=0,底边所在直线l2的方程是x+y-1=0,点(-2,0)在另一腰上,求该腰所在直线l3的方程.
【答案】
分析:设l
1、l
2、l
3的斜率分别为k
1、k
2、k
3,l
1到l
2的角是θ
1,l
2到l
3的角是θ
2,求出tanθ
1的值,根据tanθ
1=tanθ
2求得
k
3的值,用点斜式求出直线l
3的方程.
解答:解:设l
1、l
2、l
3的斜率分别为k
1、k
2、k
3,l
1到l
2的角是θ
1,l
2到l
3的角是θ
2,
则k
1=

,k
2=-1,tanθ
1=
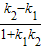
=
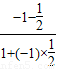
=-3.
∵l
1、l
2、l
3所围成的三角形是等腰三角形,∴θ
1=θ
2,tanθ
1=tanθ
2=-3,
即
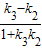
=-3,
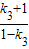
=-3,解得k
3=2. 又∵直线l
3经过点(-2,0),
∴直线l
3的方程为y=2(x+2),即2x-y+4=0.
点评:本题考查用点斜式求直线方程的方程,一条直线到另一直线的角的计算公式,求出另一腰所在线的斜率k
3的值是解题的关键.

 ,k2=-1,tanθ1=
,k2=-1,tanθ1=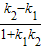 =
=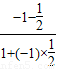 =-3.
=-3.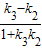 =-3,
=-3,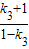 =-3,解得k3=2. 又∵直线l3经过点(-2,0),
=-3,解得k3=2. 又∵直线l3经过点(-2,0),
