
在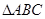 中,若
中,若 、
、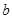 、
、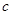 分别为角
分别为角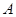 、
、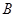 、
、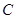 的对边,且
的对边,且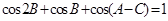 ,则有 ( )
,则有 ( )
A.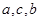 成等比数列 成等比数列 | B.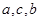 成等差数列 成等差数列 |
C.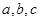 成等差数列 成等差数列 | D.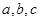 成等比数列 成等比数列 |
D
解析考点:正弦定理;等比关系的确定.
专题:计算题.
分析:把已知的等式变形后,利用诱导公式及二倍角的余弦函数公式化简,再利用和差化积公式变形后,利用正弦定理可得出ac=b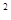 ,进而确定出a,b,c成等比数列.
,进而确定出a,b,c成等比数列.
解答:解:由cos2B+cosB+cos(A-C)=1变形得:cosB+cos(A-C)=1-cos2B,
∵cosB=cos[π-(A+C)]=-cos(A+C),cos2B=1-2sin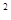 B,
B,
∴上式化简得:cos(A-C)-cos(A+C)=2sin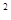 B,
B,
∴-2sinAsin(-C)=2sin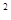 B,即sinAsinC=sin
B,即sinAsinC=sin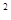 2B,
2B,
由正弦定理a :sinA ="b" :sinB ="c" :sinC 得:ac=b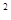 ,
,
则a,b,c成等比数列.
故选D
点评:此题考查了正弦定理,诱导公式,二倍角的余弦函数公式,和差化积公式,以及等比数列的性质,熟练掌握定理及公式是解本题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2010-2011学年河北省高三第一次月考理科数学卷 题型:选择题
在 中,若
中,若 、
、 、
、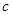 分别为角
分别为角 、
、 、
、 的对边,且
的对边,且 ,则有( )
,则有( )
A. 成等比数列
B.
成等比数列
B. 成等差数列
成等差数列
C. 成等差数列
D.
成等差数列
D. 成等比数列
成等比数列
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三第一次月考理科数学卷 题型:选择题
在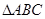 中,若
中,若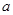 、
、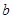 、
、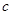 分别为角
分别为角 、
、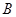 、
、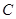 的对边,且
的对边,且 ,则有( )
,则有( )
A.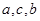 成等比数列
B.
成等比数列
B.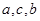 成等差数列
成等差数列
C. 成等差数列
D.
成等差数列
D. 成等比数列
成等比数列
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三第一次调研考试数学理卷 题型:选择题
在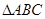 中,若
中,若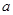 、
、 、
、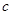 分别为角
分别为角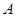 、
、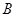 、
、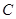 的对边,且
的对边,且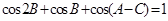 ,则有 ( )
,则有 ( )
A.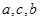 成等比数列
B.
成等比数列
B.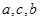 成等差数列
成等差数列
C.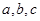 成等差数列
D.
成等差数列
D.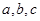 成等比数列
成等比数列
查看答案和解析>>
科目:高中数学 来源:浙江省菱湖中学2010-2011学年高三10月月考数学理 题型:选择题
在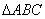 中,若
中,若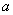 、
、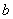 、
、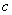 分别为角
分别为角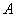 、
、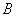 、
、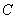 的对边,且
的对边,且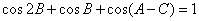 ,则有 ( )
,则有 ( )
A.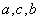 成等比数列
B.
成等比数列
B.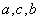 成等差数列
成等差数列
C.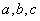 成等差数列
D.
成等差数列
D.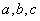 成等比数列
成等比数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com