练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

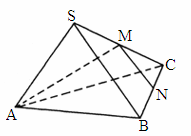
    (汕头联考模拟)如下图所示，在正三棱锥S－ABC中(底面是正多边形，顶点在底面上的射影是底面的中心的棱锥为正棱锥)，M、N分别是棱SC，BC的中点，且MN⊥AM，若侧棱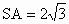，则此正三棱锥S—ABC外接球的表面积是

    [　　]

    A．45π

    B．32π

    C．12π

    D．36π
    答案：D
    解析：

    由正三棱锥的性质知SB⊥AC，又MN⊥AM．于是SB⊥平面SAC，∠ASB=∠BSC=∠CSA=90°，正三棱锥S－ABC补成以SA，SB，SC为棱的正方体，它们的外接球相同，则，R=3，则此正三棱锥S－ABC外接球的表面积是，故选D．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    (上海联考模拟)如图所示，要使火车安全行驶，按规定，铁道转弯处的圆弧半径不允许小于600m．如果某段铁路两端A，B相距800m，弧所对的圆心角小于180°，试确定圆弧弓形的高CD所允许的取值范围(精确到1m)．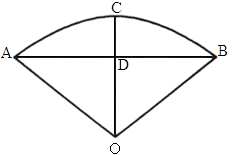

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (娄底联考模拟)如下图，在四棱锥P－ABCD中．底面ABCD为直角梯形，且AB∥CD，AB⊥AD，AD=CD=2AB=2．侧面△PAD为正三角形，且平面PAD⊥平面ABCD．

    (1)若M为PC上一动点，则M在何位置时，PC⊥平面MDB?并加已证明；

    (2)若G为△PBC的重心，求二面角G－BD－C的大小．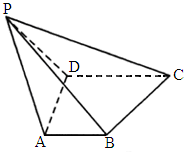

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (广东六校联考模拟)如下图，四棱锥P－ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．

    (1)求证：CD⊥AE；

    (2)求证：PD⊥平面ABE：,

    (3)求二面角A－PD－C的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

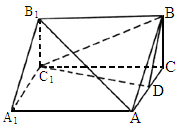
    (汕头联考模拟)如下图，三棱柱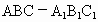中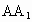，⊥面ABC，BC⊥AC，BC=AC=2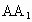，=3，D为AC的中点．

    (1)求证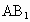：∥面；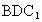

    (2)求二面角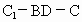的余弦值；

    (3)在侧棱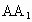上是否存在点P，使得CP⊥面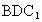?并证明你的结论．

    查看答案和解析>>

    同步练习册答案