Question

5．设质点沿以原点为圆心，半径为2的圆作匀角速度运动，角速度为$\frac{π}{60}$rad/s，试以时间t为参数，建立质点运动轨迹的参数方程．

Answer 1

分析 首先，根据题意，画出图形，然后，引入参数，建立参数方程．

解答 解：如图所示：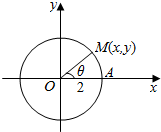

运动开始时，质点位于点A处，此时，t=0，
设动点M（x，y）对应时刻为，则
$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}\right.$，
又∵$θ=\frac{π}{60}t$，（t的单位为：秒），
故参数方程为：
$\left\{\begin{array}{l}{x=2cos\frac{π}{60}t}\\{y=2sin\frac{π}{60}t}\end{array}\right.$（t为参数）．

点评 本题重点考查了参数方程的建立，合理引入参数是解题的关键，属于中档题．