
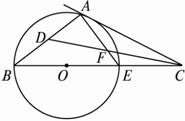
图2-4-19
(1)求∠ADF的度数.
(2)若∠ACB的度数为y度,∠B的度数为x度,那么y与x之间有怎样的关系?试写出你的猜测并给出证明.
(3)若AB =AC,求AC∶BC.
思路分析:(1)中由AC为⊙O切线可得∠B =∠EAC,由CD平分∠ACB可得∠ACD =∠DCB,根据三角形外角定理,得到∠ADF =∠AFD,建立等腰三角形,再由顶角求底角;(2)中则利用三角形内角和定理得到方程,获得关系;(3)中求线段的比值,利用△ACE∽△ABC可得.
解:(1)∵AC为⊙O的切线,?
∴∠B =∠EAC.?
∵CD平分∠ACB,?
∴∠ACD =∠DCB.?
∴∠B +∠DCB=∠EAC+∠ACD,即∠ADF =∠AFD.?
∵BE为⊙O的直径,?
∴∠DAE =90°.?
∴∠ADF =![]() (180°-∠DAE )=45°.?
(180°-∠DAE )=45°.?
(2)∵∠B =∠EAC,∠B +∠BAC+∠ACB =180°,?
∴x+90+x+y =180.?
∴y =90-2x.?
∵0<∠B<∠ADC,?
∴0<x <45.?
∴y与x的函数关系式是y =90-2x,其中x的取值范围是0<x<45.?
(3)∵∠B =∠EAC,∠ACB =∠ACB,?
∴△ACE∽△BCA.?
∴![]() =
=![]() .?
.?
∵AB =AC,?
∴∠B =∠ACB,即x =y.?
又∵y =90-2x,∴x =90-2x,x =30.?
∴在Rt△ABE中,![]() =
=![]() =tan∠ABE =tan30°=
=tan∠ABE =tan30°=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 某市教育局规定:初中升学须进行体育考试,总分30分,成绩计入初中毕业升学考试总分,还将作为初中毕业生综合素质评价“运动和健康”维度的实证材料.为了解九年级学生的体育素质,某校从九年级的六个班级共420名学生中按分层抽样抽取60名学生进行体育素质测试.
某市教育局规定:初中升学须进行体育考试,总分30分,成绩计入初中毕业升学考试总分,还将作为初中毕业生综合素质评价“运动和健康”维度的实证材料.为了解九年级学生的体育素质,某校从九年级的六个班级共420名学生中按分层抽样抽取60名学生进行体育素质测试.查看答案和解析>>
科目:高中数学 来源: 题型:
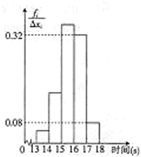 (2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
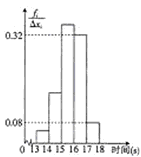 为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省皖北协作区高三(下)3月联考数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com