
【题目】已知函数![]() ,过曲线
,过曲线![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)若函数![]() 在
在![]() 处有极值,求
处有极值,求![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
科目:高中数学 来源: 题型:
【题目】为促进农业发展,加快农村建设,某地政府扶持兴建了一批“超级蔬菜大棚”,为了解大棚的面积与年利润之间的关系,随机抽取了其中的7个大棚,并对当年的利润进行统计整理后得到了如下数据对比表:

由所给数据的散点图可以看出,各样本点都分布在一条直线附近,并且![]() 与
与![]() 有很强的线性相关关系.
有很强的线性相关关系.
(1)求![]() 关于
关于![]() 的线性回归方程;(结果保留三位小数);
的线性回归方程;(结果保留三位小数);
(2)小明家的“超级蔬菜大棚”面积为8.0亩,估计小明家的大棚当年的利润为多少;
(3)另外调查了近5年的不同蔬菜亩平均利润(单位:万元),其中无丝豆为:1.5,1.7,2.1,2.2,2.5;彩椒为:1.8,1.9,1.9,2.2,2.2,请分析种植哪种蔬菜比较好?
参考数据:![]() ,
,![]() .
.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“海”“中”“加”“油”四个字,有放回地从中任取一个小球,取到“加”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1、2、3、4表示取出小球上分别写有“海”“中”“加”“油”四个字,以每两个随机数为一组,代表两次的结果.经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在极坐标系中,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() ,求直线
,求直线![]() 的极坐标方程.
的极坐标方程.
(2)已知直线![]()
![]() (
(![]() 为参数)恒经过椭圆
为参数)恒经过椭圆![]()
![]() (
(![]() 为参数)的右焦点
为参数)的右焦点![]() .
.
①求![]() 的值;
的值;
②设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与直线
与直线![]() 相切且与圆
相切且与圆![]() 外切。
外切。
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设第一象限内的点![]() 在轨迹
在轨迹![]() 上,若
上,若![]() 轴上两点
轴上两点![]() ,
,![]() ,满足
,满足![]() 且
且![]() . 延长
. 延长![]() 、
、![]() 分别交轨迹
分别交轨迹![]() 于
于![]() 、
、![]() 两点,若直线
两点,若直线![]() 的斜率
的斜率![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月份上合峰会在青岛召开,面向高校招募志愿者,中国海洋大学海洋环境学院的8名同学符合招募条件并审核通过,其中大一、大二、大三、大四每个年级各2名.若将这8名同学分成甲乙两个小组,每组4名同学,其中大一的两名同学必须分到同一组,则分到乙组的4名同学中恰有2名同学是来自于同一年级的分组方式共有__________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为探索课堂教学改革,惠来县某中学数学老师用传统教学和“导学案”两种教学方式,在甲、乙两个平行班进行教学实验.为了解教学效果,期末考试后,分别从两个班级各随机抽取20名学生的成绩进行统计,得到如下茎叶图.记成绩不低于70分者为“成绩优良”.
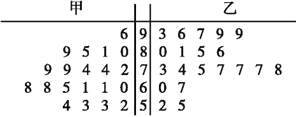
(Ⅰ)分析甲、乙两班的样本成绩,大致判断哪种教学方式的教学效果更佳,并说明理由;
(Ⅱ)由以上统计数据完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
参考公式:![]() ,其中
,其中![]() 是样本容量.
是样本容量.
独立性检验临界值表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下表:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计我校7000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将宽和长都分别为x,![]() 的两个矩形部分重叠放在一起后形成的正十字形面积为
的两个矩形部分重叠放在一起后形成的正十字形面积为![]() 注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形
注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形![]() ,
,

![]() 求y关于x的函数解析式;
求y关于x的函数解析式;
![]() 当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com