
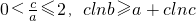 ,则下列判断正确的是
,则下列判断正确的是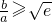
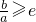
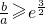
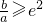
 ≥
≥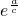 ,从而可得
,从而可得 ≥
≥
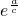 ,令t=
,令t= (t≥
(t≥ ),构造函数f(t)=
),构造函数f(t)= et,通过导数可求其最小值,从而使问题解决.
et,通过导数可求其最小值,从而使问题解决.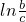 ≥a,
≥a,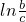 ≥
≥ ,
, ≥
≥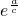 ,
, =
= •
• ≥
≥
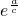
 (t≥
(t≥ ),则
),则 ≥
≥ et(t≥
et(t≥ ).
). ≤2,clnb≥a+clnc,
≤2,clnb≥a+clnc, ≥
≥ et最小值.
et最小值. et,则f′(t)=
et,则f′(t)=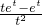 ,
, ,1]单调递减,在[1,+∞)单调递增.
,1]单调递减,在[1,+∞)单调递增. ≥e.
≥e.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| b |
| 1 |
| a |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省信阳高中高三第三次大考数学试卷(理科)(解析版) 题型:选择题
 ],则a+b=?( )
],则a+b=?( )


查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省中原名校高三(上)期中数学试卷(文科)(解析版) 题型:选择题
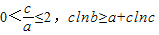 ,则下列判断正确的是( )
,则下列判断正确的是( )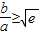
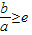
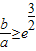
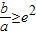
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com