(文科)袋中共有红球和白球10个,其中红球个数不少于3个,现从袋中任意取出3个球,问袋中有多少个红球时,使取得的球全为同色球的概率最小?
【答案】
分析:由题意,可设x,y分别为红球和白球的个数,则有x+y=10,x,y∈N
+,x≥3,取得的球全为同色球包括两种情况,三个球全是红色球,三个球全是白色球,分别求出这两个事件的概率,由于此两事件互斥,求出两事件概率的和的表达式,再由基本不等式计算出概率的最值
解答:解:设x,y分别为红球和白球的个数,则有x+y=10,x,y∈N
+,x≥3
从10个球中任取3个球,全为红色的概率为
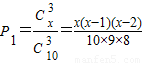
,
全为白色的概率为
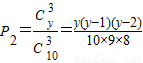
,上述两个事件互斥,故取出3个球全为同色球的概率为:
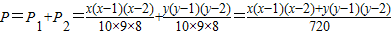
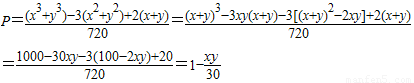
又∵x+y=10,
∴xy≤
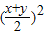
=25,此时x=y=5,
因此当x=5时,P最小,此时P=
 点评:
点评:本题考查基本不等式求最值,等可能事件的概率互斥事件的概率加法公式,排列组合在简单计数中的应用,解题的关键理解题意,将求同色球的概率的问题转化为求红色球与白色球的概率,考查了分类思想与转化的思想,运用公式进行计算的能力

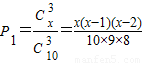 ,
,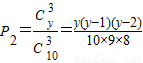 ,上述两个事件互斥,故取出3个球全为同色球的概率为:
,上述两个事件互斥,故取出3个球全为同色球的概率为: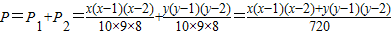
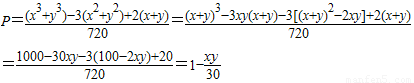
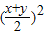 =25,此时x=y=5,
=25,此时x=y=5,


 名校课堂系列答案
名校课堂系列答案