
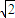 .
.
 =0 即可.以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系,再写出定点E,A,B,D的坐标,求出C点坐标,向量
=0 即可.以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系,再写出定点E,A,B,D的坐标,求出C点坐标,向量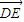 ,
,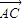 坐标,再计算(Ⅱ)
坐标,再计算(Ⅱ)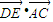 ,看是否为0.
,看是否为0.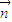 =(x,y,z) 则
=(x,y,z) 则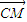 垂直于平面ADE的法向量,再利用垂直时数量积为0来计算.如能计算出参数λ的值,则存在,否则,不存在.
垂直于平面ADE的法向量,再利用垂直时数量积为0来计算.如能计算出参数λ的值,则存在,否则,不存在.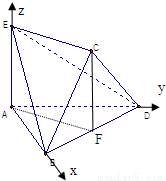 解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系
解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系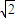 ),B(2,0,0)D(0,2,0),
),B(2,0,0)D(0,2,0),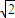
 )
)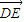 =(0,-2,
=(0,-2, ),
),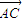 =(1,1,
=(1,1, )
) =(0,-2,
=(0,-2,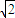 )•(1,1,
)•(1,1, )=0
)=0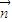 =(x,y,z) 则
=(x,y,z) 则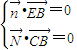 ,即
,即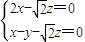 ∴
∴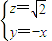
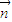 =(1,-1,
=(1,-1,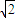 ) 又
) 又 =(0,-2,
=(0,-2,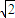 )
) 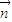 ,
,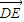 >|=
>|=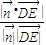 =
=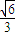
 =
=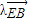
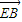 =(2,0,-
=(2,0,-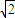 ),∴
),∴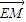 =(2λ,0,-
=(2λ,0,- ) 得M(2λ,0,
) 得M(2λ,0, )
) 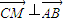 即
即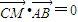



科目:高中数学 来源: 题型:
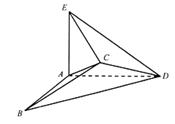
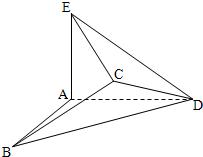 若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省金华十校高三上学期期末考试理科数学(解析版) 题型:解答题
(本题满分14分)
如图,将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且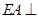 平面ABD,AE=a。
平面ABD,AE=a。
(1)若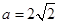 ,求证:AB//平面CDE;
,求证:AB//平面CDE;
(2)求实数a的值,使得二面角A—EC—D的大小为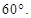
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三3月月考理科数学试卷(解析版) 题型:解答题
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
(Ⅰ)若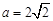 ,求证:AB//平面CDE;
,求证:AB//平面CDE;
(Ⅱ)求实数a的值,使得二面角A-EC-D的大小为60°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com