练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-1-3，圆O1与圆O2的半径都是1，|O1O2|=4，过动点P分别作圆O1、圆O2的切线PM、PN（M、N分别为切点），使得PM=PN,试建立适当的坐标系，并求动点P的轨迹方程.

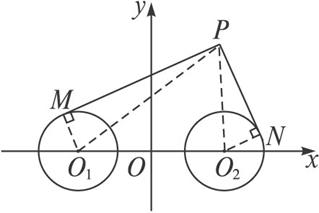
    图2-1-3

    思路分析：本题是一道很综合的题目.由题意建立坐标系，写出相关点的坐标，由几何关系式：PM=PN，即(PM)2=2(PN)2，结合图形由勾股定理转化为PO12-1=2(PO22-1).设P(x，y),由距离公式写出代数关系式，化简整理可得.

    解：如图，以直线O1O2为x轴，线段O1O2的垂直平分线为y轴，建立平面直角坐标系，则两圆心的坐标分别为O1(-2,0),O2(2,0).

    设P(x,y)，则PM2=PO12-MO12=(x+2)2+y2-1.同理,PN2=(x-2)2+y2-1.

    ∵PM=PN，∴(x+2)2+y2-1=2［(x-2)2+y2-1］，

    即x2-12x+y2+3=0，即(x-6)2+y2=33.这就是动点P的轨迹方程.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网A．（不等式选做题）若关于x的不等式|x+3|-|x+2|≥log2a有解，则实数a的取值范围是：
     
    ．
    B．（几何证明选做题）如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P．若
    PB
    PA
    =
    1
    2
    ，
    PC
    PD
    =
    1
    3
    ，则
    BC
    AD
    的值为
     
    ．
    C．（坐标系与参数方程选做题）设曲线C的参数方程为
    x=3+2
    		2
    cosθ
    y=-1+2
    		2
    sinθ
    （θ为参数），以原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρ=
    2
    cosθ-sinθ
    ，则曲线C上到直线l距离为
    		2
    的点的个数为：
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （考生注意：从下列三题中任选一题，多选的只按照第一题计分）
    ①对任意x∈R，|2-x|+|3+x|≥a2-4a恒成立，则a满足
    [-1，5]
    [-1，5]
    ．
    ②在极坐标系中，点P（2，-
    π
    6
    ）到直线l：ρsin（θ-
    π
    6
    ）=1的距离是
    		3
    +1
    		3
    +1
    ；
    ③如图，点P在圆O直径AB的延长线上，且PB=OB=2，PC切圆O于点C，CD⊥AB于点D，则CD=
    		3
    		3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）在极坐标系（ρ，θ）（0≤θ＜2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为
    		2
    ，
    3π
    4
    		2
    ，
    3π
    4
    ．
    （2）如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P，若
    PB
    PA
    =
    1
    2
    ，
    PC
    PD
    =
    1
    3
    ，则
    BC
    AD

    的值为
    		6
    6
    		6
    6
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分．
    1（1）．（几何证明选讲选做题）如图，四边形ABCD是圆O的内接四边形，
    延长AB和DC相交于点P，若
    PB
    PA
    =
    1
    2
    ，
    PC
    PD
    =
    1
    3
    ，则
    BC
    AD
    的值为
    		6
    6
    		6
    6
    ．
    （2）．（坐标系与参数方程选做题） 极坐标系中，A为曲线ρ2+2ρcosθ-3=0上
    的动点，B为直线ρcosθ+ρsinθ-7=0的动点，则|AB|距离的最小值为
    4
    		2
    -2
    4
    		2
    -2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•枣庄一模）如图，CDEF是以圆O为圆心，半径为1的圆的内接正方形，将一颗豆子随机地扔到该圆内，用A表示事件“豆子落在扇形OCFH内”（点H将劣弧
    EF
    二等分），则事件A发生的概率P（A）=（　　）

    查看答案和解析>>

    同步练习册答案