


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源:福建省清流一中2007-2008学年12月月考高三数学试卷 题型:013
(文科学生做).设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,当a∈[-1,1]时,则t的取值范围是
A.-2≤t≤2
B.![]()
C.t≥2或t≤-2或t=0
D.![]()
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省师大附中高二下学期期中考查数学卷 题型:填空题
(文科学生做)下列四个命题中,假命题有 个
① 若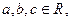 则“
则“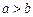 ”是“
”是“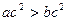 ”成立的充分不必要条件;
”成立的充分不必要条件;
② 当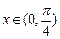 时,函数
时,函数 的最小值为2;
的最小值为2;
③若函数f(x+1)定义域为[-2,3),则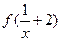 的定义域为
的定义域为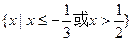 ;
;
④将函数y=cos2x的图像向右平移个单位,得到y=cos(2x-)的图像.
⑤若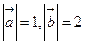 ,向量
,向量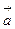 与向量
与向量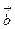 的夹角为
的夹角为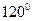 ,则
,则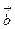 在向量
在向量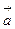 上的投影为1
上的投影为1 
查看答案和解析>>
科目:高中数学 来源:2012届安徽省高二下学期期中考查数学卷 题型:填空题
(文科学生做)下列四个命题中,假命题有 个
① 若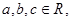 则“
则“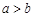 ”是“
”是“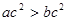 ”成立的充分不必要条件;
”成立的充分不必要条件;
② 当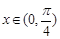 时,函数
时,函数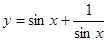 的最小值为2;
的最小值为2;
③若函数f(x+1)定义域为[-2,3),则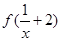 的定义域为
的定义域为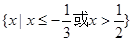 ;
;
④将函数y=cos2x的图像向右平移个单位,得到y=cos(2x-)的图像.
⑤若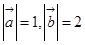 ,向量
,向量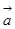 与向量
与向量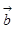 的夹角为
的夹角为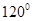 ,则
,则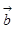 在向量
在向量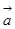 上的投影为1
上的投影为1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com