(Ⅰ)证明:令b=0,则f(a+0)=f(a)f(0),∴f(0)=1.
令b=-a,则f(0)=f(a)f(-a)=1,∴f(-a)=
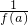
设x
1<x
2,则

=f(x
2)f(-x
1)=f(x
2-x
1),
∵x
2-x
1>0,∴0<f(x
2-x
1)<1,即:0<

<1,
设x<0,则-x>0,∴0<f(-x)<1,∴0<

<1,∴f(x)>1
∴在R上,函数f(x)>0
∴f(x)是减函数;
(Ⅱ)解:∵

,∴f(2)=f(1+1)=f(1)f(1)=

∴不等式
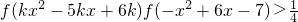
为f(kx
2-5kx+6k)•f(-x
2+6x-7)>f(2)
∴(k-1)x
2-(5k-6)x+6k-7<2
∴(k-1)x
2-(5k-6)x+6k-9<0
∴[(k-1)x-(2k-3)](x-3)<0
①k=1,不等式可化为x-1<2,所以x<3,即不等式的解集为(-∞,3);
②

;
③
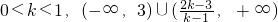
;
④

;
⑤k=0,(-∞,3)∪(3,+∞).
(Ⅲ)证明:因为f(x)在[-1,1]单调递减,f(-1)=2,
所以只需证
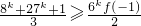
,即

,即
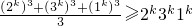
,得证.
分析:(Ⅰ)赋值,利用单调性的定义,设x
1<x
2,证明0<

<1,即可得到函数f(x)在(-∞,+∞)上为减函数;
(Ⅱ)求得f(2)=f(1+1)=f(1)f(1)=

,不等式化为[(k-1)x-(2k-3)](x-3)<0,分类讨论,即可得到结论;
(Ⅲ)利用分析法,求得f(-1)=2,只需证
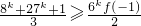
,即

,即
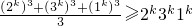
,从而得证.
点评:本题考查函数单调性的证明,考查解不等式,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

 .
.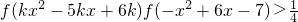 (k∈R);
(k∈R);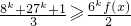 (k∈R).
(k∈R).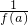
 =f(x2)f(-x1)=f(x2-x1),
=f(x2)f(-x1)=f(x2-x1), <1,
<1, <1,∴f(x)>1
<1,∴f(x)>1 ,∴f(2)=f(1+1)=f(1)f(1)=
,∴f(2)=f(1+1)=f(1)f(1)=
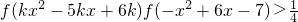 为f(kx2-5kx+6k)•f(-x2+6x-7)>f(2)
为f(kx2-5kx+6k)•f(-x2+6x-7)>f(2) ;
;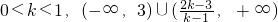 ;
; ;
;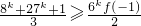 ,即
,即 ,即
,即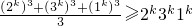 ,得证.
,得证. <1,即可得到函数f(x)在(-∞,+∞)上为减函数;
<1,即可得到函数f(x)在(-∞,+∞)上为减函数; ,不等式化为[(k-1)x-(2k-3)](x-3)<0,分类讨论,即可得到结论;
,不等式化为[(k-1)x-(2k-3)](x-3)<0,分类讨论,即可得到结论;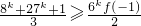 ,即
,即 ,即
,即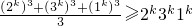 ,从而得证.
,从而得证.

 备战中考寒假系列答案
备战中考寒假系列答案