
分析 (1)利用等差数列与等比数列的通项公式即可得出;
(2)利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)设数列{an}的公差为d(d≠0),数列{bn}的公比为q,
∵由题意得a${\;}_{3}^{2}$=a1a21,∴(1+2d)2=1×(1+20d),即4d2-16d=0,
∵d≠0,∴d=4,∴an=4n-3.
(2)∵由(1)可得anbn=(4n-3)3n-1,
∴Sn=30+5×31+9×32+…+(4n-7)×3n-2+(4n-3)×3n-1,
3Sn=31+5×32+9×33+…+(4n-7)×3n-1+(4n-3)×3n,
两式相减得:
-2Sn=1+4×3+4×32+4×33+…+4×3n-1-(4n-3)×3n
=1+4(3+32+33+…+3n-1)-(4n-3)×3n
=1+$\frac{4×3×(1-3n-1)}{1-3}$-(4n-3)×3n=(5-4n)×3n-5,
∴Sn=$\frac{(4n-5)3n+5}{2}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
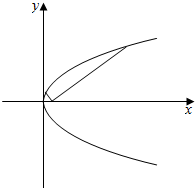 已知顶点在原点,焦点F在x轴上的抛物线过点A(9,6).
已知顶点在原点,焦点F在x轴上的抛物线过点A(9,6).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
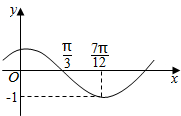 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com