分析:(Ⅰ)
Sn=na1+d=n+=n2+n,由
Sk2=(Sk)2得
k4- k3=0,又k是正整数,所以k=4.
(Ⅱ)设数列
的公差为d,则在
Sk2=(Sk)2中分别取k=1,2得
| | a1=a12,① | | 4a1+6d=(2a1+d)2,② |
| |
,由此能求出只有3个满足条件的无穷等差数列.
解答:解:(Ⅰ)∵首项a
1=
,公差d=1.
∴
Sn=na1+d=n+=n2+n,
由
Sk2=(Sk)2得
(k2)2+k2=(k2+k )2,
即
k4- k3=0,
∵k是正整数,∴k=4.…(5分)
(Ⅱ)设数列
的公差为d,
则在
Sk2=(Sk)2中分别取k=1,和k=2得
,
即
| | a1=a12,① | | 4a1+6d=(2a1+d)2,② |
| |
由①得a
1=0或a
1=1,
当a
1=0时,代入②得d=0或d=6.若a
1=0,d=0则本题成立;
若a
1=0,d=6,则a
n=6(n-1),
由S
3=18,(S
3)
2=324,S
9=216知S
9≠(S
3)
2,故所得数列不符合题意;
当a
1=1时,代入②得4+6d=(2+d)
2,
解得d=0或d=2.
若a=1,d=0则a
n=1,S
n=n从而
Sk2=(Sk)2成立;
若a
1=1,d=2,则a
n=2n-1,S
n=n
2,
从而
Sk2=(Sk)2成立.
综上所述,只有3个满足条件的无穷等差数列:
①a
n=0; ②a
n=1;③a
n=2n-1.
点评:本题考查等差数列的性质和应用,具体涉及到等差数列的前n项和公式和通项公式的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化



 ,区间M=[a,b](a<b),集合N={y|y=f(x),x
,区间M=[a,b](a<b),集合N={y|y=f(x),x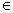 M},则使M=N成立的实数对(a,b)有
M},则使M=N成立的实数对(a,b)有