
 时,x=1,不过第一象限,故m=
时,x=1,不过第一象限,故m= .1-2m≠0,即m≠
.1-2m≠0,即m≠ 时,y=
时,y=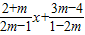 ,由此能求出m的范围.
,由此能求出m的范围.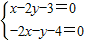 得
得 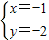 ,直线必过定点(-1,-2).由此能求出m的范围.
,直线必过定点(-1,-2).由此能求出m的范围.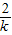 -1|,OB=|k-2|,…(8分)S△AOB=
-1|,OB=|k-2|,…(8分)S△AOB= •OA•OB=
•OA•OB= |(
|(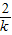 -1)(k-2)|=
-1)(k-2)|= |-
|-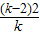 |,由此能求出△AOB面积的最小值和此时直线的方程.
|,由此能求出△AOB面积的最小值和此时直线的方程. 时,x=1,不过第一象限,∴m=
时,x=1,不过第一象限,∴m= .
. 时,
时,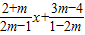 ,
,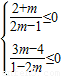 ,
,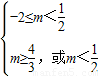 ,
,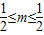 .
.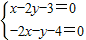 得
得  ,
, ,
,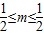 .
.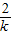 -1|,OB=|k-2|,…(8分)
-1|,OB=|k-2|,…(8分) •OA•OB=
•OA•OB= |(
|(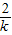 -1)(k-2)|=
-1)(k-2)|= |-
|-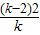 |..…(10分)
|..…(10分) [-
[-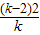 ]=
]= [4+(-
[4+(-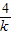 )+(-k)]≥4.
)+(-k)]≥4.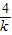 =-k,即k=-2时取等号.…(13分)
=-k,即k=-2时取等号.…(13分)

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省黄冈中学高三(上)期中数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com