
设函数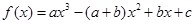 其中
其中
(1)若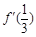 =0,求
=0,求 的单调区间;
的单调区间;
(2)设 表示
表示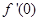 与
与 两个数中的最大值,求证:当0≤x≤1时,|
两个数中的最大值,求证:当0≤x≤1时,|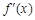 |≤
|≤ .
.
(1),函数f(x)的单调增区间是(-∞, )及(1,+∞) .单调减区间是
)及(1,+∞) .单调减区间是
(2)根据导数判定单调性,进而得到最值,然后来证明结论。
【解析】
试题分析:解:(1)由 =0,得a=b.
=0,得a=b.
当 时,则
时,则 ,
, 不具备单调性 ..2分
不具备单调性 ..2分
故f(x)= ax3-2ax2+ax+c.
由 =a(3x2-4x+1)=0,得x1=
=a(3x2-4x+1)=0,得x1= ,x2=1. 3分
,x2=1. 3分
列表:
|
x |
(-∞, |
|
( |
1 |
(1,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
f(x) |
增 |
极大值 |
减 |
极小值 |
增 |
由表可得,函数f(x)的单调增区间是(-∞, )及(1,+∞) .单调减区间是
)及(1,+∞) .单调减区间是 …5分
…5分
(2)当 时,
时, =
=
若
 ,
,
若 ,或
,或 ,
, 在
在 是单调函数,
是单调函数, ≤
≤ ≤
≤ ,或
,或

 ≤
≤ ≤
≤ 7分
7分
所以, ≤
≤
当 时,
时, =3ax2-2(a+b)x+b=3
=3ax2-2(a+b)x+b=3 .
.
①当 时,则
时,则 在
在 上是单调函数,
上是单调函数,
所以 ≤
≤ ≤
≤ ,或
,或 ≤
≤ ≤
≤ ,且
,且 +
+ =a>0.
=a>0.
所以

 . 9分
. 9分
②当 ,即-a<b<2a,则
,即-a<b<2a,则 ≤
≤ ≤
≤ .
.
(i) 当-a<b≤ 时,则0<a+b≤
时,则0<a+b≤ .
.
所以 
 =
= =
= ≥
≥ >0.
>0.
所以 

 .
11分
.
11分
(ii) 当 <b<2a时,则
<b<2a时,则 <0,即a2+b2-
<0,即a2+b2- <0.
<0.
所以 =
= >
> >0,即
>0,即 >
> .
.
所以 

 .
13分
.
13分
综上所述:当0≤x≤1时,| |≤
|≤ . 14分
. 14分
考点:导数的运用
点评:主要是对于导数再研究函数中的运用,通过判定单调性,极值来得到最值,进而求解,属于中档题。


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com