
实验表明,某型号的汽车每小时的耗油量 (升)与速度
(升)与速度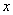 (千米/小时)的关系式为
(千米/小时)的关系式为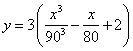 ,已知甲乙两地相距180千米,最高时速为
,已知甲乙两地相距180千米,最高时速为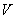 千米/小时。
千米/小时。
(1)当车速度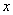 (千米/小时)时,从甲地到乙地的耗油量为
(千米/小时)时,从甲地到乙地的耗油量为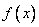 (升),求函数
(升),求函数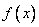 的解析式并指出函数的定义域;
的解析式并指出函数的定义域;
(2)当车速为多大时,从甲地到乙地的耗油量最少?
科目:高中数学 来源: 题型:
| x3 |
| 903 |
| x |
| 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
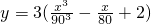 ,已知甲乙两地相距180千米,最高时速为V千米/小时.
,已知甲乙两地相距180千米,最高时速为V千米/小时.查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省连云港市高二(上)期末数学试卷(理科)(解析版) 题型:解答题
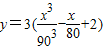 ,已知甲乙两地相距180千米,最高时速为V千米/小时.
,已知甲乙两地相距180千米,最高时速为V千米/小时.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x3 |
| 903 |
| x |
| 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com