【题目】如图，在四棱锥中， ，，是的中点，是棱上的点，，，，.

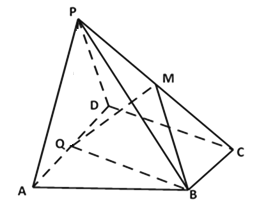
（1）求证：平面底面；

（2）设，若二面角的平面角的大小为，试确定的值.

参考答案：

【答案】见解析

【解析】(1)证明：∵，，是的中点，∴，则四边形为平行四边形，从而.∵，∴. ……2分

∵，，是的中点，∴.又∵，，∴，即，又，∴平面，∴平面底面.……5分

(2) 解：∵,是的中点,∴.∵平面平面，且平面平面，∴平面.如图，以为原点建立空间直角坐标系.

则平面的法向量为.，，，.……7分

设，则，，∵，∴，则，即，.在平面中，， ，设平面的法向量为，由，得 ，取，得.∴平面的一个法向量为. …10分

∵二面角的平面角的大小为，∴，解得.……12分.

【命题意图】本题主要考查空间直线与平面垂直、平面与平面垂直、直线与直线垂直的判定与性质，二面角等基础知识，考查学生的空间想象能力,推理论证能力,运算求解能力，以及数形结合思想、化归与转化思想．

关闭