Question

用0，1，2，…，9这10个数字，

(1)可以组成多少个五位数？

(2)可以组成多少个没有重复数字的五位数？

(3)可以组成多少个没有重复数字且能够被5整除的五位数？

Answer 1

【解】　(1)第1步　首位数字可以在1～9这9个数字中选择，有9种可能；

第2步　其他4个数位可以在0～9这10个数字中选择，有10×10×10×10＝10⁴种可能．

根据分步计数原理知，用0，1，2，…，9这10个数字，一共可以组成9×10⁴＝90 000个五位数．

(2)由于组成的五位数中不能有重复数字，所以除要考虑到首位不是0外，还要考虑到各个数位上的数字互不相同，因此，采用分步计数的方法，先确定首位数字再确定其他数位．

第1步　首位数字可以在1～9这9个数字中选择，有9种可能；

第2步　其他4个数位可以在剩下的9个数字中选择，有A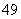种可能．

根据分步计数原理知，用0，1，2，…，9这10个数字，一共可以组成9·A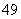＝27 216个没有重复数字的五位数．

(3)能够被5整除的数，末位有且仅有0或5两种可能，分2类进行计数．

第1类　末位是0，由于没有重复数字，所以其他4个数位共有A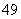＝3 024种可能；

第2类　末位是5，对其他4个数位进行分步计数：

第1步　由于首位不能为0，首位有C种可能；

第2步　其他3个数位有A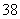种可能．

所以，第2类共有C·A＝2 688种可能．

因此，用0，1，2，…，9这10个数字，一共可以组成3 024＋2 688＝5 712个没有重复数字且能够被5整除的五位数．