
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
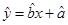 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。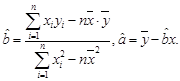 )
) 科目:高中数学 来源: 题型:解答题
某单位为了提高员工素质,举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如图所示的茎叶图(单位:分),分数在175分以上(含175分)者定为“运动健将”,并给予特别奖励,其他人员则给予“运动积极分子”称号.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人,然后再从这10人中选4人,求至少有1人是“运动健将”的概率;
(2)若从所有“运动健将”中选3名代表,求所选代表中女“运动健将”恰有2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某大学高等数学老师上学期分别采用了 两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如下:
两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如下:
(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学,求成绩为90分的同学被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| | 甲班 | 乙班 | 合计 |
| 优秀 | | | |
| 不优秀 | | | |
| 合计 | | | |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 其中
其中 )
)  为这2人所得的总奖金,求
为这2人所得的总奖金,求 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |

 ;
; )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: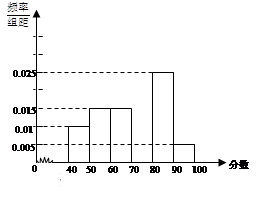
(1)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格);
(3)把90分以上(包括90分)视为成绩优秀,那么从成绩是60分以上(包括60分)的学生中选一人,求此人成绩优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在+ ~
~ (不含80)之间,属于酒后驾车;在
(不含80)之间,属于酒后驾车;在 (含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
(1)绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);
(2)求检测数据中醉酒驾驶的频率;
(3)估计检测数据中酒精含量的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题10分)某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:110, 115, 90, 85, 75, 115, 110。
(Ⅰ)这种抽样方法叫做什么抽样方法?
(Ⅱ)将这两组数据用茎叶图表示出来;
(Ⅲ)将两组数据比较:说明哪个车间的产品较稳定。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次实验,得到数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 关于
关于 的线性回归方程
的线性回归方程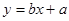 ;
; ,
, ,
,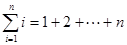
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:
性别与对景区的服务是否满意 单位:名
| | 男 | 女 | 总计 |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
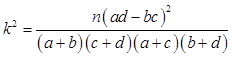
P(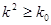 ) ) | 0.05 | 0.025 | 0.010 | 0.005 |
 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com