
分析 (1)化简集合A,B,利用集合C={x|x∈A∪B,且x∉A∩B},求集合C;
(2)设集合D={x|3-a<x<2a-1},满足A∪D=A,D⊆A,分类讨论求实数a的取值范围.
解答 解:(1)集合A={x|0<$\frac{x-1}{3}$≤1}=(1,4],B={y|y=($\frac{1}{2}$)x,且x<-1}=(2,+∞);
∴A∪B=(1,+∞);A∩B=(2,4],
∴集合C={x|x∈A∪B,且x∉A∩B}=(1,2]∪(4,+∞);
(2)∵A∪D=A,
∴D⊆A
D=∅,3-a≥2a-1,∴a≤$\frac{4}{3}$,
D≠∅,$\left\{\begin{array}{l}{3-a<2a-1}\\{3-a≥1}\\{2a-1≤4}\end{array}\right.$,∴$\frac{4}{3}$<a≤2.
综上,a≤2
点评 本题考查集合的运算与关系,考查集合的化简,正确计算是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
设数列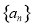 的前
的前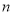 项和为
项和为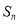 ,
,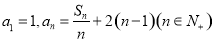 .
.
(1)证明:数列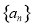 为等差数列,并分别求出
为等差数列,并分别求出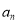 和
和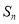 ;
;
(2)设数列 的前
的前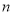 项和为
项和为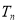 ,证明:
,证明: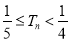 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 16 | C. | 9 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com