
分析 由①a∥b,b?α,a可能在α内,则①错误;
对于②,a∥b、a∥α,则b∥α或b?α,②错误;
对于③若a∥α,b?α,则a∥b或a,b异面,故③错误;
由④若a⊥α,b⊥α,则a∥b.垂直于同一平面的两直线平行.故④正确,
解答 解:①a∥b,b?α,a可能在α内,则①错误;
②a∥b,a∥α,则b∥α或b在平面α内,故②错误;
③若a∥α,b?α,则a∥b或a,b异面,故③错误;
④若a⊥α,b⊥α,则a∥b.垂直于同一平面的两直线平行.故④正确,
故答案为:④.
点评 本题考查空间中直线与直线、直线与平面、平面与平面的位置关系,解题时要认真审题,仔细解答,注意空间想象能力的培养,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 9 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
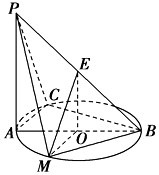 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [2,+∞) | C. | [$\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,$\frac{5}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com