解:(Ⅰ)将

cosB-

cosA=cos

=

利用正弦定理化简得:
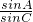
cosB-
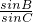
cosA=

,即2sinAcosB-2sinBcosA=sinC,
又sinC=sin[π-(A+B)]=sin(A+B),
∴2sinAcosB-2sinBcosA=sin(A+B)=sinAcosB+cosAsinB,
整理得:sinAcosB=3sinBcosA,
∴tanA=3tanB,又tanA=ktanB,
则k=3;
(Ⅱ)设tanB=t(t>0),则tanA=3t,
∵

+3t≥2

(当且仅当

=3t,即t=

时取等号),
∴tan(A-B)=
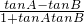
=
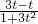
=
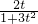
=
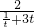
≤

,
∴tanB=t=

,tanA=3t=

,
∴B=

,A=

,
则C=

,即△ABC为直角三角形.
分析:(Ⅰ)利用正弦定理化简已知的等式,变形后再利用诱导公式及两角和与差的正弦函数公式化简,整理后利用同角三角函数间的基本关系得出tanA=3tanB,由tanA=ktanB,得出k的值为3;
(Ⅱ)由tanA=3tanB,设tanA=t(t>0),得到tanB=3t,利用两角和与差的正切函数公式化简tan(A-B),将设出的tanA及tanB代入,整理后利用基本不等式变形求出tan(A-B)的最大值,以及此时t的值,确定出tanA和tanB的值,利用特殊角的三角函数值确定出A和B的度数,利用三角形的内角和定理求出C的度数,即可判断出三角形的形状.
点评:此题考查了正弦定理,两角和与差的正弦、正切函数公式,诱导公式,以及基本不等式的运用,熟练掌握定理及公式是解本题的关键.

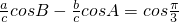 .
. cosB-
cosB- cosA=cos
cosA=cos =
= 利用正弦定理化简得:
利用正弦定理化简得: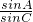 cosB-
cosB-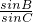 cosA=
cosA= ,即2sinAcosB-2sinBcosA=sinC,
,即2sinAcosB-2sinBcosA=sinC, +3t≥2
+3t≥2 (当且仅当
(当且仅当 =3t,即t=
=3t,即t= 时取等号),
时取等号),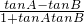 =
=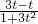 =
=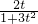 =
=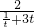 ≤
≤ ,
, ,tanA=3t=
,tanA=3t= ,
, ,A=
,A= ,
, ,即△ABC为直角三角形.
,即△ABC为直角三角形.
