
 的最高点D的坐标为(
的最高点D的坐标为( ,2),由最高点D运动到相邻最低点时,函数图象与x的交点的坐标为(
,2),由最高点D运动到相邻最低点时,函数图象与x的交点的坐标为( ,0)。
,0)。 的解析式;
的解析式;  时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值;
的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值; 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 的单调减区间。
的单调减区间。 科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011内蒙古高一第二学期期中考试理数 题型:解答题
. (12分)
设y=A sin(ωx+j)(A>0,ω>0,|j|<π)最高点D的坐标为(2,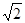 ),由最高点运动到相邻的最低点时,曲线与
),由最高点运动到相邻的最低点时,曲线与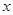 轴交点E的坐标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.
轴交点E的坐标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)设y=A sin(ωx+j)(A>0,ω>0,|j|<π)最高点D的坐标为(2,![]() ),由最高点运动到相邻的最低点时,曲线与
),由最高点运动到相邻的最低点时,曲线与![]() 轴交点E的坐标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.
轴交点E的坐标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com