Question

如图，AB为圆O的直径，点E、F在圆O上，且AB∥EF，矩形ABCD所在的平面与圆O所在的平面互相垂直，已知AB＝2，AD＝EF＝1．

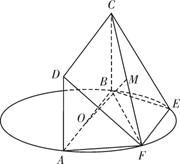
（Ⅰ）设FC的中点为M，求证：OM∥平面DAF；

（Ⅱ）设平面CBF将几何体EF-ABCD分割成的两个锥体的体积分别为V_F-ABCD、V_F-CBE，求V_F-ABCD：V_F-CBE的值．

 

Answer 1

【答案】

（Ⅰ）详见解析；（Ⅱ）4.

【解析】

试题分析：（Ⅰ）在平面内找一条直线与已知直线平行，通过线线平行可证；（Ⅱ）通过等体积法来求；

试题解析：（Ⅰ）如图，设FD的中点为N，连结AN，MN．

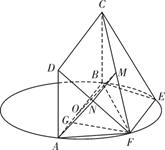
∵M为FC的中点，

∴MN∥CD，MN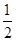＝CD．

又AO∥CD，AO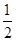＝CD，

∴MN∥AO，MN＝AO，

∴MNAO为平行四边形，

∴OM∥AN，

又OM⊄平面DAF，AN⊂平面DAF，

∴OM∥平面DAF．                        6分

（Ⅱ）如图，过点F作FG⊥AB于G．

∵平面ABCD⊥平面ABEF，

∴FG⊥平面ABCD，

∴V_F-ABCD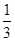＝S_ABCD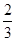·FG＝FG．

∵CB⊥平面ABEF，

∴V_F-CBE＝V_C-BEF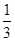＝S_△BEF·CB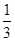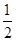＝·EF·FG·CB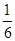＝FG．

∴V_F-ABCD：V_F-CBE＝4．                       13分

考点：线面平行的证明；椎体的体积求法.