
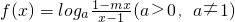 的图象关于原点对称.
的图象关于原点对称.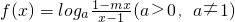 的图象关于原点对称
的图象关于原点对称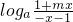 +
+ =0对定义域内任意x都成立,
=0对定义域内任意x都成立,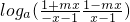 =loga1,
=loga1,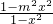 =1对定义域内任意x都成立,
=1对定义域内任意x都成立,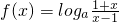 ,(x>1)
,(x>1)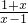 ,再令1<x1<x2,则t1=
,再令1<x1<x2,则t1=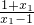 ,t2=
,t2=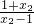 ,
,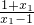 -
-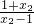 =
=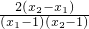 >0,有t1>t2,
>0,有t1>t2,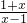 是(1,+∞)上的减函数.
是(1,+∞)上的减函数.

科目:高中数学 来源: 题型:022
(
山东胜利一中模拟)已知下列命题:A.![]() ;
;
B.函数f(|x|-1)的图象向左平移1个单位后得到的函数图象解析式为y=f(|x|);
C.函数y=f(1+x)的图象与函数y=f(1-x)的图象关于y轴对称;
D.满足条件 ,∠B=60°,AB=1的△ABC有两个.其中正确命题的代号是_________.(按照原顺序将所有正确命题的代号都写出来)
,∠B=60°,AB=1的△ABC有两个.其中正确命题的代号是_________.(按照原顺序将所有正确命题的代号都写出来)
查看答案和解析>>
科目:高中数学 来源: 题型:022
(2006
北京东城模拟)已知函数 ,给出下列命题:
,给出下列命题:
A.f(x)不可能为偶函数;
B.当f(0)=f(2)时,f(x)的图象必关于直线x=1对称;
C.若 ,则f(x)在区间[a,+∞)上是增函数;
,则f(x)在区间[a,+∞)上是增函数;
D.f(x)
有最小值 ,其中正确命题的代号是________(按照原顺序将你认为正确的命题的代号都填上).
,其中正确命题的代号是________(按照原顺序将你认为正确的命题的代号都填上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com