
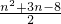 ,求C1,C2,C3;
,求C1,C2,C3; ,…1′
,…1′ .…3′
.…3′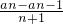 =1,∴Cn-1 =
=1,∴Cn-1 =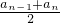 =
=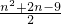 .…5′
.…5′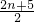 -λ•
-λ•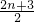 =(1-λ)n+
=(1-λ)n+ -
- λ=常数,
λ=常数,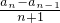 =
=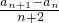 ,…10′∴
,…10′∴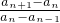 =
=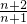 .
.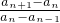 •
•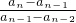 …
…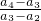 •
•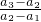 =
=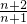 •
• …
… •
• =
= .
. (a2-a1)•(n+2),…12′
(a2-a1)•(n+2),…12′ (a2-a1)•(n+1),
(a2-a1)•(n+1), (a2-a1)×4,
(a2-a1)×4, (a2-a1)×3,
(a2-a1)×3, (a2-a1)•
(a2-a1)•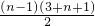 (n≥2)
(n≥2) (a2-a1)(n-1)(n+4)+a1(n≥2).…14′
(a2-a1)(n-1)(n+4)+a1(n≥2).…14′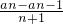 =1,可得Cn-1 的值,再根据等差数列的定义求得满足条件的λ.
=1,可得Cn-1 的值,再根据等差数列的定义求得满足条件的λ.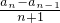 =
=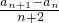 ,即
,即 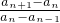 =
=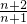 ,用累乘法求得an+1-an=
,用累乘法求得an+1-an= (a2-a1)•(n+2),再用累加法求得满足条件的
(a2-a1)•(n+2),再用累加法求得满足条件的

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| anan+2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | anan+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com