
已知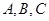 是球面上三点,且
是球面上三点,且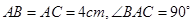 ,若球心
,若球心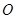 到平面
到平面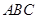 的距离为
的距离为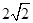 ,则该球的表面积为__________
,则该球的表面积为__________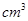 .
.
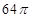
【解析】
试题分析:由已知中球面上有A、B、C三点,AB=AC=2,∠BAC=90°,我们可以求出平面ABC截球所得截面的直径BC的长,进而求出截面圆的半径r,根据已知中球心到平面ABC的距离,根据球的半径R=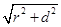 ,求出球的半径,代入球的表面积公式,即可得到答案。解:由已知中AB=AC=2,∠BAC=90°,我们可得BC为平面ABC截球所得截面的直径,即2r=
,求出球的半径,代入球的表面积公式,即可得到答案。解:由已知中AB=AC=2,∠BAC=90°,我们可得BC为平面ABC截球所得截面的直径,即2r=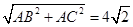
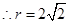 ,又球心
,又球心 到平面
到平面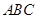 的距离为
的距离为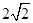 ,那么可知球的半径R=
,那么可知球的半径R=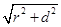 =4,∴球的表面积S=4π?R2=
=4,∴球的表面积S=4π?R2=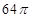 ,故答案为:
,故答案为: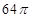
考点:球的表面积
点评:本题考查的知识点是球的表面积,其中根据球半径,截面圆半径,球心距,构成直角三角形,满足勾股定理,求出球的半径是解答本题的关键


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013年上海市黄浦区高考数学二模试卷(理科)(解析版) 题型:填空题
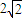 ,则该球的表面积为 cm3.
,则该球的表面积为 cm3.查看答案和解析>>
科目:高中数学 来源:2011年四川省成都七中高考考前热身数学试卷(文科)(解析版) 题型:选择题
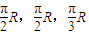 ,则四面体OABC的体积为( )
,则四面体OABC的体积为( )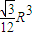
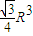
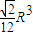
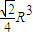
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com