Question

椭圆E的中心在原点O，焦点在x轴上，其离心率e=,过点C（-1，0）的直线l与椭圆E相交于A、B两点，且满足点C分向量的比为2.

（1）用直线l的斜率k(k≠0)表示△OAB的面积；

（2）当△OAB的面积最大时，求椭圆E的方程.

Answer 1

解：（1）设椭圆E的方程为+=1,(a＞b＞0),由e==得，a²=3b².

    故椭圆方程为x²+3y²=3b².

    设A（x₁,y₁）、B（x₂、y₂）.由于点C（-1，0）分向量的比为2，

∴

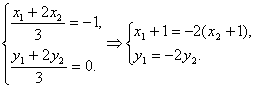
    由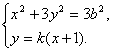(3k²+1)x²+6k²x+3k²-3b²=0.

    由直线l与椭圆E相交于A（x₁,y₁)、B(x₂,y₂)两点得：

    而S_△OAB=|y₁-y₂|=|-2y₂-y₂|=|y₂|=|k(x₂+1)|,    ①

    由=-1和x₁+x₂=得x₂+1=,把其代入①得：

S_△OAB=(k≠0).

（2）因S_△OAB==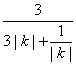≤=,当且仅当k=±时，S_△OAB取得最大值，此时x₁+x₂=-1.

    又∵ =1,∴x₂=-3,x₁=1,将x₁=1,x₂=-3,k=±代入x₁x₂=,

    得3b²=5.

∴椭圆方程为x²+3y²=5.