
已知数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对任意给定的![]() ,是否存在
,是否存在![]() (
(![]() )使
)使![]() 成等差数列?若存在,用
成等差数列?若存在,用![]() 分别表示
分别表示![]() 和
和![]() (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为![]() .
.
【解】(1)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以![]() ;
;
综上所述,![]() . ……………………3分
. ……………………3分
(2)当![]() 时,若存在p,r使
时,若存在p,r使![]() 成等差数列,则
成等差数列,则![]() ,
,
因为![]() ,所以
,所以![]() ,与数列
,与数列![]() 为正数相矛盾,因此,当
为正数相矛盾,因此,当![]() 时不存在; ……5分
时不存在; ……5分
当![]() 时,设
时,设![]() ,则
,则![]() ,所以
,所以![]() ,………………7分
,………………7分
令![]() ,得
,得![]() ,此时
,此时![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ;
;
综上所述,当![]() 时,不存在p,r;当
时,不存在p,r;当![]() 时,存在
时,存在![]() 满足题设.
满足题设.
……………………10分
(3)作如下构造:![]() ,其中
,其中![]() ,
,
它们依次为数列![]() 中的第
中的第![]() 项,第
项,第![]() 项,第
项,第![]() 项, ……12分
项, ……12分
显然它![]() 们成等比数列,且
们成等比数列,且![]() ,
,![]() ,所以它们能组成三角形.
,所以它们能组成三角形.
由![]() 的任意性,这样的三角形有无穷多个. ……………………14分
的任意性,这样的三角形有无穷多个. ……………………14分
下面用反证法证明其中任意两个三角形![]() 和
和![]() 不相似:
不相似:
若三角形![]() 和
和![]() 相似,且
相似,且![]() ,则
,则![]() ,
,
整理得![]() ,所以
,所以![]() ,这与条件
,这与条件![]() 相矛盾,
相矛盾,
因此,任意两个三角形不相似.
故命题成立. ……………………16分
【注】1.第(2)小题当ak不是质数时,p,r的解不唯一;
2. 第(3)小题构造的依据如下:不妨设![]() ,且
,且![]() 符合题意,则公比
符合题意,则公比![]() >1,因
>1,因![]() ,又
,又![]() ,则
,则![]() ,所以
,所以![]() ,因为三项均为整数,所以
,因为三项均为整数,所以![]() 为
为![]() 内的既约分数且
内的既约分数且![]() 含平方数因子,经验证,仅含
含平方数因子,经验证,仅含![]() 或
或![]() 时不合,所以
时不合,所以![]() ;
;
3.第(3)小题的构造形式不唯一.


科目:高中数学 来源:2014届陕西省高二上学期期末考试理科数学试卷(解析版) 题型:解答题
已知数列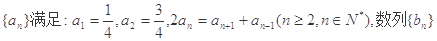 满足:
满足: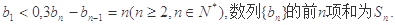
(1)求证:数列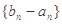 为等比数列;
为等比数列;
(2)求证:数列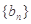 为递增数列;
为递增数列;
(3)若当且仅当 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南通市高三第二次模拟考试数学试题 题型:解答题
已知数列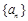 满足
满足 .
.
(1)求数列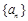 的通项公式;
的通项公式;
(2)对任意给定的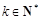 ,是否存在
,是否存在 (
(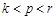 )使
)使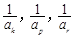 成等差数列?若存
成等差数列?若存
在,用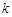 分别表示
分别表示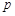 和
和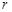 (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为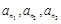 .
.
查看答案和解析>>
科目:高中数学 来源:2010年湖北省高二12月月考数学试卷 题型:解答题
已知数列 满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
(1)求a2、a3
(2)猜想 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高二下学期期中考试数学(理) 题型:解答题
(14分)已知数列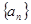 满足
满足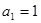 ,
,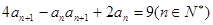
(1)求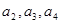 。(2)由(1)猜想
。(2)由(1)猜想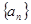 的通项公式。(3)用数学归纳法证明(2)的结果。[来源:学#科#网]
的通项公式。(3)用数学归纳法证明(2)的结果。[来源:学#科#网]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com