
如图,直角坐标系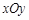 中,一直角三角形
中,一直角三角形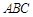 ,
,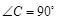 ,B、D在
,B、D在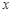 轴上且关于原点
轴上且关于原点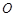 对称,
对称,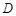 在边
在边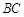 上,BD=3DC,△ABC的周长为12.若一双曲线
上,BD=3DC,△ABC的周长为12.若一双曲线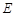 以B、C为焦点,且经过A、D两点.
以B、C为焦点,且经过A、D两点.
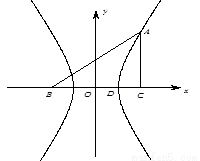
⑴ 求双曲线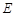 的方程;
的方程;
⑵ 若一过点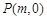 (
(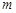 为非零常数)的直线
为非零常数)的直线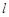 与双曲线
与双曲线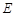 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点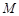 、
、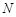 ,且
,且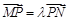 ,问在
,问在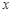 轴上是否存在定点
轴上是否存在定点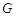 ,使
,使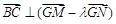 ?若存在,求出所有这样定点
?若存在,求出所有这样定点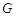 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
(1) 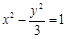 (2)在
(2)在 轴上存在定点
轴上存在定点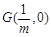 ,使
,使 .
.
【解析】
试题分析:(1) 设双曲线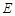 的方程为
的方程为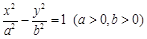 ,则
,则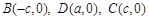 .
.
由 ,得
,得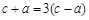 ,即
,即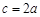 .
.
∴ 3分
3分
解之得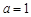 ,∴
,∴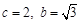 .
.
∴双曲线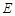 的方程为
的方程为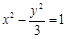 . 5分
. 5分
(2) 设在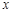 轴上存在定点
轴上存在定点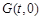 ,使
,使 .
.
设直线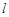 的方程为
的方程为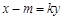 ,
,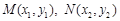 .
.
由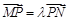 ,得
,得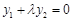 .
.
即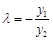 ①
6分
①
6分
∵ ,
,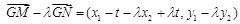 ,
,
∴
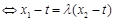 .
.
即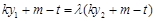 . ② 8分
. ② 8分
把①代入②,得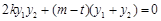 ③
9分
③
9分
把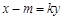 代入
代入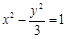 并整理得
并整理得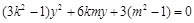
其中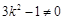 且
且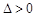 ,即
,即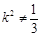 且
且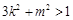 .
.
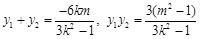 . 10分
. 10分
代入③,得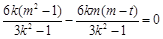 ,化简得
,化简得 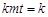 .当
.当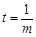 时,上式恒成立.
时,上式恒成立.
因此,在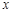 轴上存在定点
轴上存在定点 ,使
,使 . 13分
. 13分
考点:本题主要考查双曲线的方程,直线与双曲线的位置关系,平面向量的坐标运算。
点评:难题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(1)求双曲线方程时,应用了双曲线的定义及其几何性质,难度不大,较为典型。(2)则在应用韦达定理的基础上,通过平面向量的坐标运算,达到证明目的。


科目:高中数学 来源: 题型:
 设f(x)是定义在R上的偶函数,当0≤x≤2时,y=x,当x>2时,y=f(x)的图象是顶点为P(3,4),且过点A(2,2)的抛物线的一部分.
设f(x)是定义在R上的偶函数,当0≤x≤2时,y=x,当x>2时,y=f(x)的图象是顶点为P(3,4),且过点A(2,2)的抛物线的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:
 某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 语文(x分) | 89 | 91 | 93 | 95 | 97 |
| 英语(y分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:
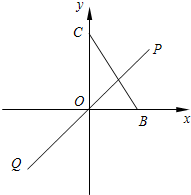 如图,直角坐标系中,B在x轴上、C在y轴上,且|BC|=a (a>0),若长为2a的线段PQ以原点O为中点,问
如图,直角坐标系中,B在x轴上、C在y轴上,且|BC|=a (a>0),若长为2a的线段PQ以原点O为中点,问| PQ |
| BC |
| BP |
| CQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•深圳一模)一次考试中,五名同学的数学、物理成绩如下表所示:
(2013•深圳一模)一次考试中,五名同学的数学、物理成绩如下表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学(x分) | 89 | 91 | 93 | 95 | 97 |
| 物理(y分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com