
如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2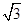 ,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为
,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为 
 。
。
【解析】
试题分析:因为∠BAD=90°,所以AD⊥AB,又AD⊥BC,且AB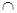 BC=B,所以AD⊥平面ABC。
BC=B,所以AD⊥平面ABC。
在平面ABC内,取点P,连PA,则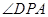 是DP与平面ABC所成角。
是DP与平面ABC所成角。
又因为AD=4,所以直线DP与平面ABC所成角的正切值为2,须AP=2,即点P在△ABC内所成的轨迹是以A为圆心,半径为2 的圆的一部分。
而∠BAC=120°=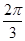 ,故点P在△ABC内所成的轨迹的长度为
,故点P在△ABC内所成的轨迹的长度为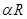 =
= 。
。
考点:本题主要考查立体几何中的垂直关系,角的计算,圆的定义,扇形弧长公式。
点评:典型题,综合性较强,考查知识全面,可谓之是“证算并重题”,较好地考查了数形结合思想及学生的逻辑推理能力、计算能力。解答本题的关键是认识到“点P在△ABC内所成的轨迹是以A为圆心,半径为2 的圆的一部分。”


科目:高中数学 来源: 题型:
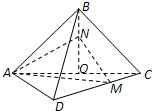 已知正方形ABCD的边长为2
已知正方形ABCD的边长为2| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年云南省昭通市毕业生复习统一检测文科数学试卷(解析版) 题型:选择题
已知正方形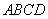 的边长为
的边长为 ,将
,将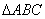 沿对角线
沿对角线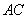 折起,使平面
折起,使平面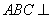 平面
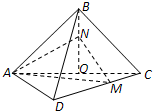
平面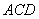 ,得到如图所示的三棱锥
,得到如图所示的三棱锥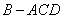 .若
.若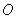 为
为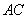 边的中点,
边的中点,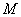 ,
, 分别为线段
分别为线段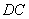 ,
, 上的动点(不包括端点),且
上的动点(不包括端点),且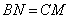 .设
.设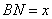 ,则三棱锥
,则三棱锥 的体积
的体积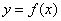 的函数图象大致是
的函数图象大致是
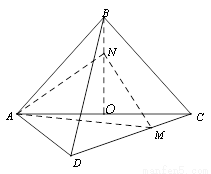

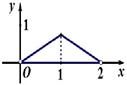
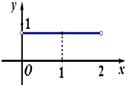

A. B. C. D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市朝阳区高三上学期期末考试理科数学 题型:选择题
已知正方形 的边长为
的边长为 ,将
,将 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,得到如图所示的三棱锥
,得到如图所示的三棱锥 .若
.若 为
为 边的中点,
边的中点, ,
, 分别为线段
分别为线段 ,
, 上的动点(不包括端点),且
上的动点(不包括端点),且 .设
.设 ,则三棱锥
,则三棱锥 的体积
的体积 的函数图象大致是( )
的函数图象大致是( )
A.  B.
B.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 2 |
A.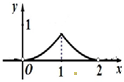 | B.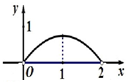 | C.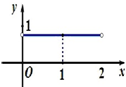 | D.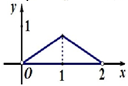 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com