
| A£® | 45¡ă | B£® | 60¡ă | C£® | 120¡ă | D£® | 135¡ă |
·ÖÎö ÓĂ$\overrightarrow{AB}$£¬$\overrightarrow{AC}$±íʾ³ö$\overrightarrow{CD}£¬\overrightarrow{BE}$£¬¸ù¾ƯÊưÁ¿»ưÁĐ³ö·½³̀Çó³ö$\overrightarrow{AB}•\overrightarrow{AC}$£¬´úÈë¼Đ½Ç¹«Ê½¼ÆËăcosA£®
½â´đ ½â£º$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\frac{3}{4}\overrightarrow{AB}$£¬$\overrightarrow{BE}$=$\overrightarrow{BA}+\frac{2}{3}\overrightarrow{AC}$£¬
¡à$\overrightarrow{CD}$•$\overrightarrow{BE}$=£¨$\overrightarrow{CA}$+$\frac{3}{4}\overrightarrow{AB}$£©£¨$\overrightarrow{BA}+\frac{2}{3}\overrightarrow{AC}$£©=-$\frac{3}{4}$$\overrightarrow{AB}$2-$\frac{2}{3}$$\overrightarrow{AC}$2+$\frac{3}{2}$$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{3}{4}$-$\frac{4}{3}$+$\frac{3}{2}$$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{43}{12}$£¬
¡à$\overrightarrow{AB}•\overrightarrow{AC}$=-1£®
¡àcosA=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{AB•AC}$=-$\frac{\sqrt{2}}{2}$£¬¡àA=135¡ă£®
¹ÊÑ¡D£®
µăÆÀ ±¾̀⿼²éÁËƽĂæỊ̈Á¿µÄÊưÁ¿»ưÔËËă£¬Ị̈Á¿µÄÏßĐÔÔËËă£¬ÊôÓÚ»ù´¡̀⣮


 ÔĶÁ¿́³µÏµÁĐ´đ°¸
ÔĶÁ¿́³µÏµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | $\frac{1}{2}$ | B£® | 2 | C£® | -2 | D£® | -$\frac{1}{2}$ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | Ơ棬?x0¡ÊR£¬cosx0£¾1 | B£® | Ơ棬?x¡ÊR£¬cosx£¾1 | ||
| C£® | ¼Ù£¬?x0¡ÊR£¬cosx0£¾1 | D£® | ¼Ù£¬?x¡ÊR£¬cosx£¾1 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 0 | B£® | 1 | C£® | 2 | D£® | 3 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
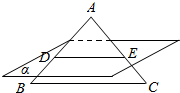 Èçͼ£¬̉ÑÖª¡÷ABCÊDZ߳¤Îª2µÄƠưÈư½ÇĐΣ¬OÊÇËüµÄÖĐĐÄ£¬¹ưµăO×÷BCƽĐеÄƽĂæ¦Á£¬·Ö±đ½»AB£¬ACÓÚµăD£¬E£¬ỘËıßĐÎBCEDµÄĂæ»ưÊÇ£¨¡¡¡¡£©
Èçͼ£¬̉ÑÖª¡÷ABCÊDZ߳¤Îª2µÄƠưÈư½ÇĐΣ¬OÊÇËüµÄÖĐĐÄ£¬¹ưµăO×÷BCƽĐеÄƽĂæ¦Á£¬·Ö±đ½»AB£¬ACÓÚµăD£¬E£¬ỘËıßĐÎBCEDµÄĂæ»ưÊÇ£¨¡¡¡¡£©| A£® | $\frac{5\sqrt{3}}{9}$ | B£® | $\frac{4\sqrt{3}}{9}$ | C£® | $\frac{\sqrt{3}}{3}$ | D£® | $\frac{2\sqrt{3}}{3}$ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | -1-2i | B£® | -1+2i | C£® | 1+2i | D£® | 1-2i |
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com