
分析 (1)解绝对值不等式可得不等式|x-m|<|x|的解集为(1,+∞),可得1是方程2mx=m2的解,由此求得m的值.
(2)由题意可得不等式a-5<|x+1|-|x-2|<a+2对x∈(0,+∞)恒成立,结合f(x)=|x+1|-|x-2|∈(-1,3],可得a+2>3,a-5≤-1,由此求得a的范围.
解答 解:(1)由|x-m|<|x|得|x-m|2<|x|2,即2mx>m2,而不等式|x-m|<|x|的解集为(1,+∞),
∴1是方程2mx=m2的解,解得m=2(m=0舍去).
(2)∵m=2,∴不等式$\frac{a-5}{x}<|{1+\frac{1}{x}}|-|{1-\frac{m}{x}}|<\frac{a+2}{x}$对x∈(0,+∞)恒成立,
等价于不等式a-5<|x+1|-|x-2|<a+2对x∈(0,+∞)恒成立.
设$f(x)=|{x+1}|-|{x-2}|=\left\{\begin{array}{l}2x-1,0<x<2\\ 3,x≥2\end{array}\right.$,则f(x)∈(-1,3].
∴a+2>3,且a-5≤-1,∴1<a≤4.
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,求函数的值域,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .. | B. | $\frac{9}{8}$ | C. | $\frac{8}{9}$ | D. | $\frac{25}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
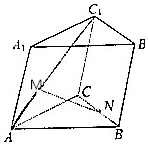 如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).
如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
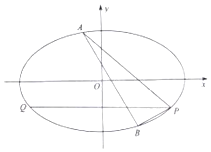 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-y+8=0 | B. | x-3y+8=0 | C. | 3x+y+8=0 | D. | 3x+y+4=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com