
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
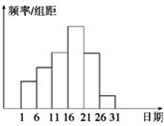 在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形高的比为2:3:4:6:4:1,第三组的频数为12,则本次活动参加评比作品总数、上交的作品数量最多的组的作品件数依次为( )
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形高的比为2:3:4:6:4:1,第三组的频数为12,则本次活动参加评比作品总数、上交的作品数量最多的组的作品件数依次为( )| A、60、18 | B、60、20 | C、80、18 | D、80、30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
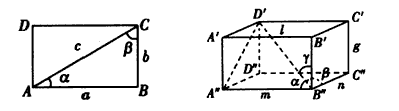
 (2012•芜湖二模)设长方形ABCD边长分别是AD=1,AB=2(如图所示),点P在△BCD内部和边界上运动,设
(2012•芜湖二模)设长方形ABCD边长分别是AD=1,AB=2(如图所示),点P在△BCD内部和边界上运动,设| AP |
| AB |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•日照一模)已知长方形EFCD,|EF|=2,|FC|=
(2013•日照一模)已知长方形EFCD,|EF|=2,|FC|=
| ||
| 2 |
| FA |
| FB |
| TA |
| TB |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省湛江市高三8月第一次月考理科数学试卷(解析版) 题型:解答题
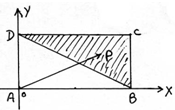
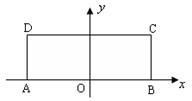
(本小题满分14分)已知长方形 ,
,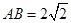 ,
,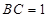 ,以
,以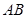 的中点
的中点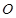 为
为
原点建立如图所示的平面直角坐标系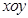 .
.
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)设椭圆上任意一点为P,在x轴上有一个动点Q(t,0),其中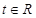 ,探究
,探究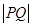 的最
的最
小值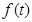 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com