
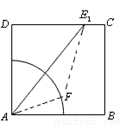
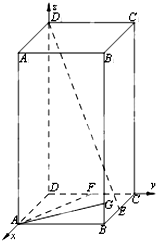
已知长方体 中,底面
中,底面 为正方形,
为正方形, 面
面 ,
, ,
, ,点
,点 在棱
在棱 上,且
上,且 .
.

(Ⅰ)试在棱 上确定一点
上确定一点 ,使得直线
,使得直线 平面
平面 ,并证明;
,并证明;
(Ⅱ)若动点 在底面
在底面 内,且
内,且 ,请说明点
,请说明点 的轨迹,并探求
的轨迹,并探求 长度的最小值.
长度的最小值.
(Ⅰ)详见解析;(Ⅱ)点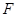 在平面
在平面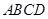 内的轨迹是以
内的轨迹是以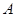 为圆心,半径等于2的四分之一圆弧,且
为圆心,半径等于2的四分之一圆弧,且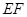 长度的最小值为
长度的最小值为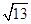 .
.
【解析】
试题分析:(Ⅰ)先利用证明四边形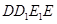 为平行四边形证明
为平行四边形证明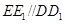 从而证明直线
从而证明直线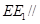 平面
平面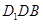 ,或者可以以
,或者可以以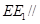 平面
平面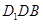 为已知条件出发,利用直线与平面平行的性质定理得到
为已知条件出发,利用直线与平面平行的性质定理得到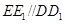 ,进而确定点
,进而确定点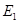 的位置;(Ⅱ)先确定四边形
的位置;(Ⅱ)先确定四边形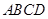 的形状以及各边的长度,然后再根据
的形状以及各边的长度,然后再根据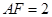 以及点
以及点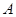 为定点这一条件确定点
为定点这一条件确定点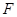 的轨迹,在计算
的轨迹,在计算 的过程中,可以利用
的过程中,可以利用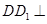 平面
平面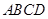 以及
以及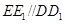 从而得到
从而得到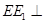 平面
平面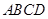 ,于是得到
,于是得到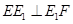 ,进而可以由勾股定理
,进而可以由勾股定理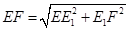 ,从而将问题转化为当
,从而将问题转化为当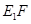 取到最小值时,
取到最小值时, 取到最小值.
取到最小值.
试题解析:(Ⅰ)取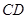 的四等分点
的四等分点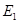 ,使得
,使得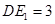 ,则有
,则有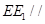 平面
平面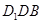 . 证明如下: 1分
. 证明如下: 1分
因为 且
且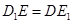 ,
,
所以四边形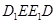 为平行四边形,则
为平行四边形,则 , 2分
, 2分
因为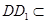 平面
平面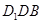 ,
,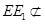 平面
平面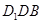 ,所以
,所以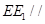 平面
平面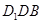 . 4分
. 4分
(Ⅱ)因为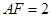 ,所以点
,所以点 在平面
在平面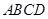 内的轨迹是以
内的轨迹是以 为圆心,半径等于2的四分之一圆弧. 6分
为圆心,半径等于2的四分之一圆弧. 6分
因为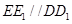 ,
, 面
面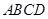 ,所以
,所以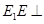 面
面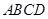 , 7分
, 7分
故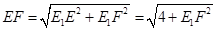 . 8分
. 8分
所以当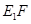 的长度取最小值时,
的长度取最小值时,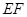 的长度最小,此时点
的长度最小,此时点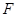 为线段
为线段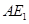 和四分之一圆弧的交点, 10分
和四分之一圆弧的交点, 10分
即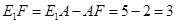 ,
,
所以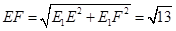 .
.
即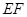 长度的最小值为
长度的最小值为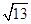 . 12分
. 12分
考点:直线与平面平行、勾股定理、点到圆上一点距离的最值


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,在长方体ABCD-A1C1B1D1中,已知上下两底面为正方形,且边长均为1;侧棱AA1=2,E为BC中点,F为CD中点,G为BB1上一个动点.
如图,在长方体ABCD-A1C1B1D1中,已知上下两底面为正方形,且边长均为1;侧棱AA1=2,E为BC中点,F为CD中点,G为BB1上一个动点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•泉州模拟)已知长方体ABCD-A1B1C1D1中,底面ABCD为正方形,D1D⊥面ABCD,AB=4,AA1=2,点E在棱C1D1上,且D1E=3.
(2013•泉州模拟)已知长方体ABCD-A1B1C1D1中,底面ABCD为正方形,D1D⊥面ABCD,AB=4,AA1=2,点E在棱C1D1上,且D1E=3.查看答案和解析>>
科目:高中数学 来源: 题型:
一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面尺寸一样,已知长方体的长、宽、高分别为20m,5m,10m,四棱锥的高为8m,若按1500的比例画出它的直观图,那么直观图中,长方体的长、宽、高和四棱锥的高应分别为( )
A.4cm,1cm,2cm,1.6cm
B.4cm,0.5cm,2cm,0.8cm
C.4cm,0.5cm,2cm,1.6cm
D.2cm,0.5cm,1cm,0.8cm
查看答案和解析>>
科目:高中数学 来源:2013届广东省六校联合体高二元月联考理科数学(解析版) 题型:选择题
已知在长方体ABCDA1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
A .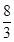 B.
B.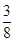 C.
C.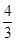 D.
D.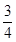
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com