
将函数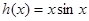 在
在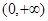 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列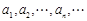 ,给出以下不等式:
①
,给出以下不等式:
①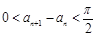 ; ②
; ②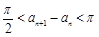 ;③
;③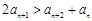 ;④
;④ ;其中,正确的判断是( )
;其中,正确的判断是( )
A. ①③ B. ①④ C. ②③ D. ②④
D
【解析】
试题分析::∵函数f(x)=xsinx,∴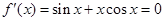 ,∴tanx=-x,
,∴tanx=-x,
∴函数f(x)在(0,+∞)内的全部极值点就是函数y=tanx与y=-x的交点的横标,
观察两条直线的交点,从纵轴向右,在每一个周期上都有一个交点,
且从左向右,交点的位置依次更靠近渐近线,
∴两个交点之间的横标之差小于一个周期,大于半个周期,故选C.
考点: 数列与三角的综合考查,导数在三角函数中的应用,正切函数的图像与性质.
点评:解本题的关键是根据导数等于零,得到tanx=-x,从而确定函数f(x)在(0,+∞)内的全部极值点就是函数y=tanx与y=-x的交点的横标,然后观察两线的交点,在每一个周期上都有一个交点,且从左向右,交点的位置更靠近渐近线,两个点之间的横标的差.


 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com