【答案】
分析:根据(1)命题的逆命题为假命题,而逆命题与否命题同真假,得到(1)不正确.(2)空间中还可以成其它的角度.(如90°),所以(2)错误.(3)若(1+x)
10=a
+a
1x+…+a
10x
10,左右两边同时对x求导,再利用赋值法即可得出结论;(4)根据函数的最值,得到不正确,(5)根据分段函数的周期性得到正确.
解答:解:(1)命题的逆命题为:x,y∈R,若x=0或y=0,则x
2+y
2=0,为假命题,
而逆命题与否命题同真假,所以(1)不正确.
(2)空间中还可以成其它的角度.(如90°),所以(2)错误.
(3)若(1+x)
10=a
+a
1x+…+a
10x
10,左右两边同时对x求导,
则10(1+x)
9=a
1+2a
2x+…+10a
10x
9,
令 x=1 则a
1+2a
2+3a
3+…+10a
10=10×2
9
∴a
+a
1+2a
2+3a
3+…+10a
10
=10×2
9+1
所以(3)错误
(4)设
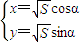
代入4x
2-5xy+4y
2=5式得:4S-5S•sinαcosα=5
解得 S=
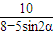
;
∵-1≤sin2α≤1
∴3≤8-5sin2α≤13
∴
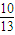
≤
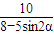
≤
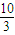
则
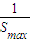
+
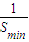
=
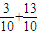
=
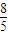
,所以(4)错误
(5)函数f(x)=
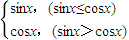
分段函数中两个函数都是周期函数,
可以得到分段函数为周期函数,且最小正周期T=2π.所以(5)正确.
故答案为:(1)(5).
点评:本题考查命题真假的判断,本题解题的关键是利用否命题与逆命题之间的同真假的关系,考查周期函数和函数的最值,本题是一个易错题.

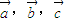 两两成的夹角均相等,则夹角为0°或120°
两两成的夹角均相等,则夹角为0°或120° +
+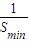 =
=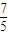
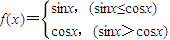 为周期函数,且最小正周期T=2π
为周期函数,且最小正周期T=2π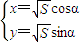 代入4x2-5xy+4y2=5式得:4S-5S•sinαcosα=5
代入4x2-5xy+4y2=5式得:4S-5S•sinαcosα=5 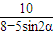 ;
;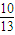 ≤
≤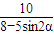 ≤
≤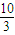
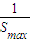 +
+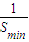 =
=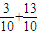 =
=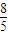 ,所以(4)错误
,所以(4)错误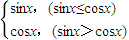 分段函数中两个函数都是周期函数,
分段函数中两个函数都是周期函数,

 备战中考寒假系列答案
备战中考寒假系列答案 如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:
如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论: 上的函数
上的函数 ,给出以下结论:
,给出以下结论: 是周期函数;(2)
是周期函数;(2) 的最小值是
的最小值是 ;(3)当且仅当
;(3)当且仅当 时,
时, 有最大值;(4)
有最大值;(4) 的图象上相邻的最低点的距离是
的图象上相邻的最低点的距离是 .
.