练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知xy=9，x≥y＞1，t=（log3x）（log3y）则（ ）
    A．0＜t≤1
    B．0＜t＜1
    C．t＞1
    D．t≥1
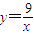
    【答案】分析：由xy=9 可得代入t=（log3x）（log3y），根据对数的运算性质可得t=（log3x）（log3y）=（-（log3x）2+2log3x 由xy=9，x≥y＞1可求3≤x＜9 进一步可得1≤log3x＜2，结合二次函数的性质可求
    解答：解：∵t=（log3x）（log3y）
    =
    =（-（log3x）2+2log3x=-（log3x-1）2+1
    ∵xy=9，x≥y＞1，
    ∴3≤x＜9，1≤log3x＜2
    ∴0＜t≤1
    故选A
    点评：本题主要考查了对数的运算性质，二次函数的在区间上的最值的求解，属于基础知识的简单综合．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知xy=9，x≥y＞1，t=（log3x）（log3y）则（　　）
    A、0＜t≤1B、0＜t＜1C、t＞1D、t≥1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知样本9，10，11，x，y的平均数是10，标准差是
    		2
    ，则xy=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知xy=9，x≥y＞1，t=（log3x）（log3y）则


    1. A.
      0＜t≤1
    2. B.
      0＜t＜1
    3. C.
      t＞1
    4. D.
      t≥1

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知xy=9，x≥y＞1，t=（log3x）（log3y）则（　　）
    A．0＜t≤1B．0＜t＜1C．t＞1D．t≥1

    查看答案和解析>>

    同步练习册答案