(本题满分14分)
解:(I)2sin
2(A+

)-

cos2A=1-cos(2A+

)-

cos2A
=1+sin2A-

cos2A=1+2(

sin2A-

cos2A)
=1+2sin(2A-

)=1+

,
∴sin(2A-

)=

,(4分)
∵A∈(0,

),2A-

∈(-

,

),
∴2A-

=

,解得A=

;(7分)
(II)根据题意画出图形,如图所示:
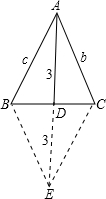
延长AD到点E,使DE=AD=3,又AD为中线,可得BD=CD,
∴四边形ABEC为平行四边形,
∴AC∥BE,BE=AC=b,
又A=

,
∴∠BAC+∠ABE=π,即∠ABE=π-∠BAC=

,
在△ABE中,根据余弦定理得:6
2=b
2+c
2-2bccos∠ABE=b
2+c
2+bc,
又b
2+c
2≥2bc,
∴bc≤
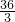
=12,(11分)
∴S
△ABC=

bcsin∠BAC=

bc≤3

,当且仅当b=c=2

时取等号,
则△ABC面积的最大值为3

.(14分)
分析:(I)把已知的等式的左边第一项利用二倍角的余弦函数公式化简,再利用诱导公式变形后,根据两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(2A-

)的值,由A为锐角,得到2A-

的范围,利用特殊角的三角函数值即可求出A的度数;
(II)根据题意画出相应的图形,延长AD到E,使DE=AD,连接BE,CE,根据对角线互相平分的四边形为平行四边形得到ABEC为平行四边形,可得出对边AC与BE平行,根据两直线平行同旁内角互补可得出∠ABE与∠BAC互补,由∠BAC的度数表示出∠ABE的度数,在三角形ABE中,由余弦定理得到AE
2=b
2+c
2-2bccos∠ABE,将AE及表示出的∠ABE的度数代入,整理后再利用基本不等式变形,求出bc的最大值,然后利用三角形的面积公式表示出三角形ABC的面积,将∠BAC的度数及bc的最大值代入即可求出面积的最大值.
点评:此题考查了余弦定理,三角形的面积公式,两角和与差的正弦函数公式,二倍角的余弦函数公式,诱导公式,基本不等式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

 )-
)- cos2A=
cos2A= .
. )-
)- cos2A=1-cos(2A+
cos2A=1-cos(2A+ )-
)- cos2A
cos2A cos2A=1+2(
cos2A=1+2( sin2A-
sin2A- cos2A)
cos2A) )=1+
)=1+ ,
, )=
)= ,(4分)
,(4分) ),2A-
),2A- ∈(-
∈(- ,
, ),
), =
= ,解得A=
,解得A= ;(7分)
;(7分)
 ,
, ,
,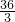 =12,(11分)
=12,(11分) bcsin∠BAC=
bcsin∠BAC= bc≤3
bc≤3 ,当且仅当b=c=2
,当且仅当b=c=2 时取等号,
时取等号, .(14分)
.(14分) )的值,由A为锐角,得到2A-
)的值,由A为锐角,得到2A- 的范围,利用特殊角的三角函数值即可求出A的度数;
的范围,利用特殊角的三角函数值即可求出A的度数;

 )-
)- cos2A=
cos2A= .
.