
已知函数 在
在 上是减函数,在
上是减函数,在 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且
上有三个零点,且 是其中一个零点.
是其中一个零点.
(1)求 的值;
的值;
(2)求 的取值范围;
的取值范围;
(3)设 ,且
,且 的解集为
的解集为 ,求实数
,求实数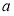 的取值范围.
的取值范围.
(1)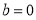 ,(2)
,(2)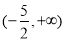 ,(3)
,(3)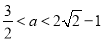
【解析】
试题分析:(1)函数在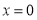 处单调性发生变化,所以
处单调性发生变化,所以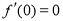 ,由
,由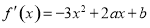 得
得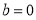 .(2)因为
.(2)因为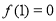 ,所以
,所以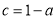 ,因此
,因此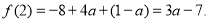 因为函数
因为函数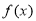 在
在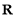 上有三个零点,所以
上有三个零点,所以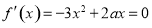 必有两个不等的根
必有两个不等的根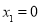 ,
,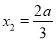 .又
.又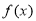 在
在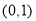 上是增函数,所以大根不小于1,即
上是增函数,所以大根不小于1,即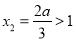 ,
,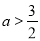 ,故
,故 的取值范围为
的取值范围为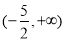 .(3)已知不等式解集求参数取值范围,有两个解题思路,一是解不等式,根据解集包含关系对应参数取值范围.二是转化,将不等式在区间有解理解为恒成立问题,利用函数最值解决参数取值范围.本题由于已知
.(3)已知不等式解集求参数取值范围,有两个解题思路,一是解不等式,根据解集包含关系对应参数取值范围.二是转化,将不等式在区间有解理解为恒成立问题,利用函数最值解决参数取值范围.本题由于已知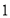 是其中一个零点,所以两个方法都简便.否则应利用变量分离求最值法.
是其中一个零点,所以两个方法都简便.否则应利用变量分离求最值法.
试题解析:(1)∵f(x)=-x3+ax2+bx+c,∴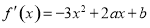 . 1分
. 1分
∵f(x)在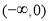 上是减函数,在
上是减函数,在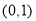 上是增函数,
上是增函数,
∴当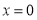 时,
时,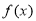 取到极小值,即
取到极小值,即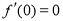 .∴
.∴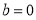 . 3分
. 3分
(2)由(1)知,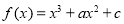 ,
,
∵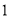 是函数
是函数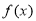 的一个零点,即
的一个零点,即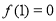 ,∴
,∴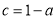 . 5分
. 5分
∵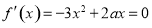 的两个根分别为
的两个根分别为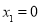 ,
,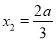 .
.
又∵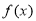 在
在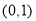 上是增函数,且函数
上是增函数,且函数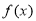 在
在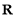 上有三个零点,
上有三个零点,
∴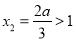 ,即
,即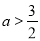 . 7分
. 7分
∴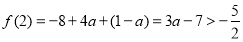 .
.
故 的取值范围为
的取值范围为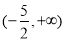 . 9分
. 9分
(3)解法1:由(2)知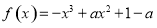 ,且
,且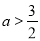 .
.
∵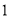 是函数
是函数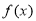 的一个零点,∴
的一个零点,∴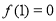 ,
,
∵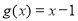 ,∴
,∴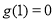 ,
,
∴点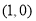 是函数
是函数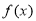 和函数
和函数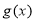 的图像的一个交点. 10分
的图像的一个交点. 10分
结合函数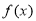 和函数
和函数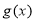 的图像及其增减特征可知,当且仅当函数
的图像及其增减特征可知,当且仅当函数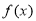 和函数
和函数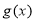 的图像只有一个交点
的图像只有一个交点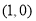 时,
时,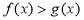 的解集为
的解集为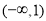 .
.
即方程组 ①只有一组【解析】
①只有一组【解析】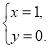 11分
11分
由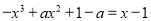 ,得
,得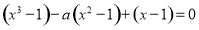 .
.
即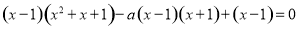 .
.
即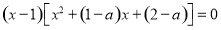 .
.
∴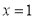 或
或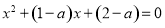 . 12分
. 12分
由方程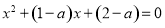 ②
②
得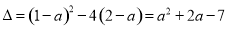 .∵
.∵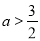 ,
,
当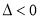 ,即
,即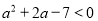 ,解得
,解得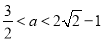 . 13分
. 13分
此时方程②无实数解,方程组①只有一个解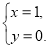
所以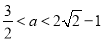 时,
时,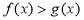 的解集为
的解集为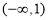 . 14分
. 14分
(3)解法2:由(2)知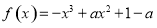 ,且
,且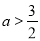 .
.
∵1是函数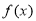 的一个零点
的一个零点
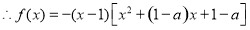
又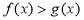 的解集为
的解集为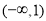 ,
,
∴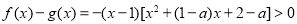 的解集为
的解集为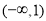 . 10分
. 10分
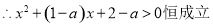 .
.
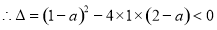 . 12分
. 12分
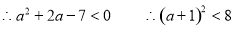 .
.
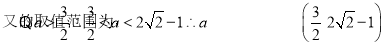 . 14分
. 14分
考点:利用导数求参数取值范围


科目:高中数学 来源:2013-2014学年陕西省高考前30天数学保温训练10复数(解析版) 题型:选择题
复数z= 的共轭复数是( )
的共轭复数是( )
A.2+i B.2﹣i C.﹣1+i D.﹣1﹣i
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省等五校高三第三次模拟理科数学试卷(解析版) 题型:选择题
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )

(A)45 (B)50
(C)55 (D)60
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省等五校高三第三次模拟文科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)在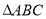 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,求
,求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高三下学期第八次适应性训练理科数学试卷(解析版) 题型:解答题
已知椭圆 经过点
经过点 .
.
(1)求椭圆 的方程及其离心率;
的方程及其离心率;
(2)过椭圆右焦点 的直线(不经过点
的直线(不经过点 )与椭圆交于
)与椭圆交于 两点,当
两点,当 的平分线为
的平分线为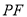 时,求直线
时,求直线 的斜率
的斜率 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com